练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，点D是等边△ABC内一点，DA＝13，DB＝19，DC＝21，将△ABD绕点A逆时针旋转到△ACE的位置，求△DEC的周长．

    【答案】53.

    【解析】

    先根据等边三角形的性质得∠BAC=60°，AB=AC，再根据旋转的性质得到AD=AE，CE=BD=19，∠DAE=∠BAC=60°，则可判断△ADE为等边三角形，从而得到DE=AD=13，然后计算△DEC的周长．

    ∵△ABC 为等边三角形，

    ∴∠BAC=60°，AB=AC，

    ∵△ABD 绕点 A 逆时针旋转到△ACE 的位置，

    ∴AD=AE，CE=BD=19，∠DAE=∠BAC=60°，

    ∴△ADE 为等边三角形，

    ∴DE=AD=13，

    ∴△DEC 的周长=DE+DC+CE=13+21+19=53．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知A，B两点的坐标分别为（2，0），（0，10），M是△AOB外接圆⊙C上的一点，且∠AOM=30°，则点M的坐标为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

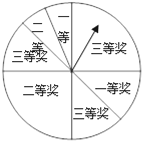
    【题目】为吸引顾客，石景山万达广场某餐饮店推出转盘抽奖打折活动，如图是可以自由转动的转盘，转盘被分成若干个扇形，转动转盘，转盘停止后，指针所指区域内的奖项可作为打折等级（若指针指向两个扇形的交线时，重新转动转盘），其中一等奖打九折，二等奖打九五折，三等奖赠送小礼品．小明和同学周六去就餐，他们转动一次转盘能够得到九折优惠的概率是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

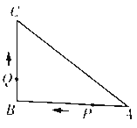
    【题目】如图，已知△ABC中，∠B=90°，AB=8 cm，BC=6 cm，P，Q是△ABC边上的两个动点，点P从点A开始沿A→B方向运动，且速度为1 cm，点Q从点B开始沿B→C方向运动，且速度为2 cm/s，它们同时出发，设运动的时间为t s.

    （1）运动几秒时，△APC是等腰三角形？

    （2）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，点F在线段CE上，且四边形BFED为菱形，则CF的为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发现：当，时，∵，∴，当且仅当时取等号．请利用上述结论解决以下问题：

    (1)当时，的最小值为_______；当时，的最大值为__________．

    (2)当时，求的最小值．

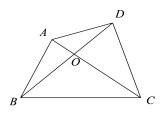
    (3)如图，四边形ABCD的对角线AC ，BD相交于点O，△AOB、△COD的面积分别为4和9，求四边形ABCD面积的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，AB＝AC，∠A＝20°，AB上一点D，且AD＝BC，过点D作DE∥BC且DE＝AB，连接EC，则∠DCE的度数为（ ）

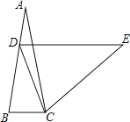
    A. 80° B. 70° C. 60° D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料：对于平面直角坐标系中的任意两点，，我们把叫做，两点间的距离公式，记作，如：，，则，两点的距离为

    请根据以上的阅读材料，解答下列问题：

    （1）当，的距离，求出的值．

    （2）若在平面内有一点，使有最小值，求出它最小值和此时的范围．

    （3）若有最小值，请直接写出最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图已知，于点，于点交于点．，，．

    （1）若，点是上一点，当点到点和点的距离相等时，求的长；

    （2）若，点是上一点，点是上一点，连接，，，求的最小值．

    查看答案和解析>>

    同步练习册答案