
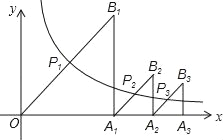
【题目】如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An﹣1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An﹣1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数![]() 的图象上,则y1+y2+y3+…+yn=_____.
的图象上,则y1+y2+y3+…+yn=_____.
【答案】![]()
【解析】
根据△OP1A1是等腰直角三角形,过点P1作P1M⊥x轴,则P1M=OM=MA1,所以可设P1的坐标是(a,a),把(a,a)代入解析式得到a=4,从而求出A1的坐标是(8,0),再根据△P2A1A2是等腰直角三角形,设P2的纵坐标是b,则P2的横坐标是8+b,把(8+b,b)代入函数解析式得到b的值,故可得出P2的纵坐标y2,同理可以得到p3的纵坐标,Pn的纵坐标,根据规律可以求出y1+y2+…yn.
解:如图,过点P1作P1M⊥x轴,
∵△OP1A1是等腰直角三角形,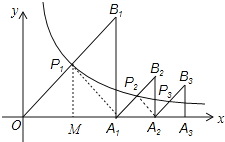
∴P1M=OM=MA1,
设P1的坐标是(a,a),把(a,a)代入解析式y=![]() (a>0)中,得a=4,
(a>0)中,得a=4,
∴y1=4,
又∵△P2A1A2是等腰直角三角形,
∴设P2的纵坐标是b(b>0),则P2的横坐标是8+b,把(8+b,b)代入函数解析式得b=![]() ,
,
解得b=4![]() -4
-4
∴y2=4![]() -4,
-4,
设P3的纵坐标是c(c>0),则P3横坐标为8+2(4![]() -4)+c=8
-4)+c=8![]() +c,把(8
+c,把(8![]() +c,c)代入函数解析式得c=
+c,c)代入函数解析式得c=![]() ,
,
解得c=4![]() -4
-4![]() ,
,
∴y3=4![]() -4
-4![]() ,
,
∵y1=4![]() -4
-4![]() ,y2=4
,y2=4![]() -4
-4![]() ,y3=4
,y3=4![]() -4
-4![]() ,…
,…
∴yn=4![]() -4
-4![]() ,
,
∴y1+y2+y3+…+yn=4+4![]() -4+4
-4+4![]() -4
-4![]() +…+4
+…+4![]() -4
-4![]() =4
=4![]() .
.
故答案为4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当![]() ,
,![]() 时,∵
时,∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号.请利用上述结论解决以下问题:
时取等号.请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为_______;当
的最小值为_______;当![]() 时,
时,![]() 的最大值为__________.
的最大值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
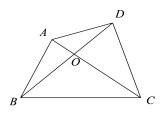
(3)如图,四边形ABCD的对角线AC ,BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
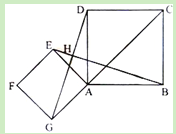
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
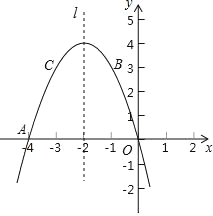
【题目】如图,已知二次函数 y=ax2+bx+c 的图象经过点 A(﹣4,0),B(﹣1,3),C(﹣3,3).
(1)求此二次函数的解析式
(2)设此二次函数的对称轴为直线 l,该图象上的点 P(m,n)在第三象限, 其关于直线 1 的对称点为 M,点 M 关于 y 轴的对称点为 N,若四边形 OAPN 的面积为 20,求 m,n 的值;
(3)在对称轴直线 l 上是否存在一点 D,使△ADC 的周长最短,如果存在,求出点 D 的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,点
,点![]() 是
是![]() 上一点,当点
上一点,当点![]() 到点
到点![]() 和点
和点![]() 的距离相等时,求
的距离相等时,求![]() 的长;
的长;
(2)若![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
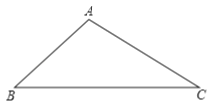
【题目】数学课上老师提出了如下问题:
尺规作图:作![]() 中
中![]() 边上的高线
边上的高线
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
作法:如图,
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)小乐和小马帮助小东完成下面的证明.
小乐:证明:![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上(依据1).
的垂直平分线上(依据1).
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() 线段
线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
小乐:证明:![]() ,
,![]() ,
,![]()
![]()
![]()
又![]()
![]() (依据2)
(依据2)
∴线段![]() 是
是![]() 中
中![]() 边上的高线
边上的高线
上述证明过程中的“依据1”和“依据2”分别指什么?
(3)请你用不同于小东的方法完成老师提出的问题.
(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 边上的高
边上的高![]() 的长度为__________.
的长度为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
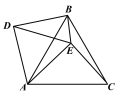
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE=![]() ,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
(1)如图1,当![]() =60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
=60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
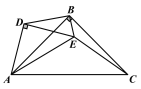
(2)如图2当![]() =90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
=90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若BC=![]() ,请直接写出△BDE的面积.
,请直接写出△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com