
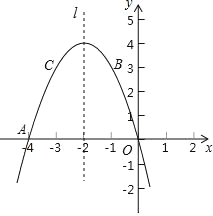
【题目】如图,已知二次函数 y=ax2+bx+c 的图象经过点 A(﹣4,0),B(﹣1,3),C(﹣3,3).
(1)求此二次函数的解析式
(2)设此二次函数的对称轴为直线 l,该图象上的点 P(m,n)在第三象限, 其关于直线 1 的对称点为 M,点 M 关于 y 轴的对称点为 N,若四边形 OAPN 的面积为 20,求 m,n 的值;
(3)在对称轴直线 l 上是否存在一点 D,使△ADC 的周长最短,如果存在,求出点 D 的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2﹣4x;(2)m 的值为﹣5,n 的值为﹣5;(3)在对称轴直线 l 上存在一点 D,使△ADC 的周长最短,点 D 的坐标为(﹣2, 2).
【解析】
(1)根据点 A、B、C 的坐标,利用待定系数法即可求出二次函数的解析式;
(2)利用配方法找出二次函数的对称轴,由点 P 的坐标可得出点 M、N 的坐标,利用梯形的面积公式结合四边形 OAPN 的面积为 20,可求出 n 值,再利用二次函数图象上点的坐标特征可求出 m 的值;
(3)连接 AB,交直线 l 于点 D,利用两点之间线段最短可得出点 D 即为所求, 根据点 A、B 的坐标,利用待定系数法可求出直线 AB 的解析式,再利用一次函数图象上点的坐标特征可求出点 D 的坐标.
解:(1)将 A(﹣4,0)、B(﹣1,3)、C(﹣3,3)代入 y=ax2+bx+c 中,
得: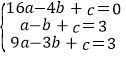 ,解得:
,解得: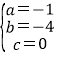 ,
,
∴二次函数的解析式为 y=﹣x2﹣4x.
(2)∵二次函数的解析式为 y=﹣x2﹣4x=﹣(x+2)2+4,
∴二次函数的对称轴为直线 x=﹣2.
∵点 P(m,n)关于直线 1 的对称点为 M,点 M 关于 y 轴的对称点为 N,
∴点 M(﹣4﹣m,n),点 N(m+4,n)(如图 1),
∴S 四边形 OAPN=![]() (OA+PN)|n|=
(OA+PN)|n|= ![]() (4+4)|n|=20, 解得:n1=5,n2=﹣5.
(4+4)|n|=20, 解得:n1=5,n2=﹣5.
∵点 P(m,n)在第三象限,
∴n=﹣5,
∴﹣m2﹣4m=﹣5,
解得:m1=﹣5,m2=1(舍去).
∴m 的值为﹣5,n 的值为﹣5.
(3)∵AC 的值为定值,
∴要使△ADC 的周长最短,则 AD+CD 的值最小.
连接 AB,交直线 l 于点 D,则 BD=CD,此时由两点之间线段最短可得知,点 D
即为所求(如图 2).
设直线 AB 的解析式为 y=kx+d(k≠0),
将 A(﹣4,0)、B(﹣1,3)代入 y=kx+d 中,
得:![]() ,解得:
,解得:![]() ,
,
∴直线 AB 的解析式为 y=x+4, 当 x=﹣2 时,y=x+4=2,
∴点 D 的坐标为(﹣2,2).
∴在对称轴直线 l 上存在一点 D,使△ADC 的周长最短,点 D 的坐标为(﹣2, 2).


科目:初中数学 来源: 题型:
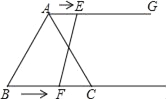
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的k倍的三角形叫做“k倍三角形”(k为正实数).
(1)理解:根据“k倍三角形”的定义填空(填“锐角”、“直角”或“钝角”):
①当![]() 时,k倍三角形一定是_____________三角形;
时,k倍三角形一定是_____________三角形;
②当![]() 时,k倍三角形一定是______________三角形.
时,k倍三角形一定是______________三角形.
(2)探究:当![]() 时,已知Rt△ABC为“k倍三角形”,且
时,已知Rt△ABC为“k倍三角形”,且![]() ,
,![]() ,求所有满足条件的k值.
,求所有满足条件的k值.
(3)拓展:若Rt△ABC是“k倍三角形”,且![]() ,
,![]() ,
,![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第四象限,随着点A的运动,点C的位置也不断变化,但点C始终在第四象限,且双曲线
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第四象限,随着点A的运动,点C的位置也不断变化,但点C始终在第四象限,且双曲线![]() 始终经过点C,则k的值为_____.
始终经过点C,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
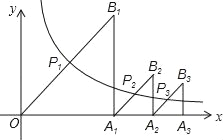
【题目】如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An﹣1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An﹣1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数![]() 的图象上,则y1+y2+y3+…+yn=_____.
的图象上,则y1+y2+y3+…+yn=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com