
【题目】阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的k倍的三角形叫做“k倍三角形”(k为正实数).
(1)理解:根据“k倍三角形”的定义填空(填“锐角”、“直角”或“钝角”):
①当![]() 时,k倍三角形一定是_____________三角形;
时,k倍三角形一定是_____________三角形;
②当![]() 时,k倍三角形一定是______________三角形.
时,k倍三角形一定是______________三角形.
(2)探究:当![]() 时,已知Rt△ABC为“k倍三角形”,且
时,已知Rt△ABC为“k倍三角形”,且![]() ,
,![]() ,求所有满足条件的k值.
,求所有满足条件的k值.
(3)拓展:若Rt△ABC是“k倍三角形”,且![]() ,
,![]() ,
,![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)①直角;②钝角;(2)3或2或5;(3)![]() 或
或![]() .
.
【解析】
(1)设三角形三边分别为a、b、c,
①当![]() 时,可以得到
时,可以得到![]() ,三边满足勾股定理即可判断三角形为直角三角形;
,三边满足勾股定理即可判断三角形为直角三角形;
②当![]() 时,可以得到
时,可以得到![]() ,可以判断三角形为钝角三角形;
,可以判断三角形为钝角三角形;
(2)当![]() 时,Rt△ABC为“k倍三角形”,由
时,Rt△ABC为“k倍三角形”,由![]() ,
,![]() ,利用勾股定理求出第三边,需要分情况讨论:当AB是斜边时;当AB是直角边时两种情况求解即可 ;
,利用勾股定理求出第三边,需要分情况讨论:当AB是斜边时;当AB是直角边时两种情况求解即可 ;
(3)若Rt△ABC是“k倍三角形”,根据题意可得三边关系式,结合勾股定理得到方程组,求解即可表示![]() 的值.
的值.
(1)设三角形三边分别为a、b、c,
①当![]() 时,可以得到
时,可以得到![]() ,则三角形是直角三角形,
,则三角形是直角三角形,
故答案为:直角;
②当![]() 时,可以得到
时,可以得到![]() ,则三角形为钝角三角形,
,则三角形为钝角三角形,
故答案为:钝角;
(2)当![]() 时,已知Rt△ABC为“k倍三角形”,且
时,已知Rt△ABC为“k倍三角形”,且![]() ,
,![]() ,分以下情况:
,分以下情况:
①当AB为斜边时,由![]() ,
,
∴![]() ,解得AC=
,解得AC=![]() ,
,
由![]() ,
,
可得:4+2=2k,
解得:k=3;
②当AB为直角边时,由![]() ,
,
∴![]() ,解得AC=
,解得AC=![]() ,
,
由![]() 或者
或者![]() ,
,
可得:6+2=4k,或者4+6=2k,
解得:k=2或者k=5,
综上所述,满足条件的k值为3或2或5;
故答案为:3或2或5;
(3)在Rt△ABC中,![]() ,
,
又∵k=2,
∴![]() 或
或![]() ,
,
∴联立方程组得
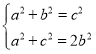 或
或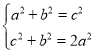 ,
,
解得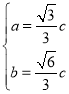 或
或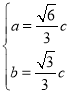 ,
,
∴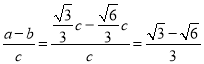 或
或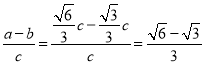 ,
,
∴![]() 的值为:
的值为:![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地之间有一条直线跑道,甲,乙两人分别从
两地之间有一条直线跑道,甲,乙两人分别从![]() 、
、![]() 同时出发,相向而行均速跑步,且乙的速度是甲速度的80%,当甲,乙两人分别到达
同时出发,相向而行均速跑步,且乙的速度是甲速度的80%,当甲,乙两人分别到达![]() 地,
地,![]() 地后立即掉头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行).甲,乙两人之间的距离
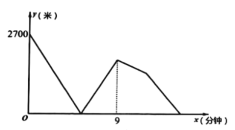
地后立即掉头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行).甲,乙两人之间的距离![]() (米)与跑步时间
(米)与跑步时间![]() (分钟)之间的关系如图所示,则他们在第二次相遇时距
(分钟)之间的关系如图所示,则他们在第二次相遇时距![]() 地___________米.
地___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
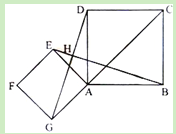
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
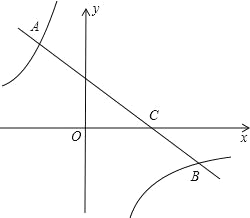
【题目】如图,一次函数 y=kx+2(k<0)的图象经过点 C(3,0),且反比例函数 y=![]() 的图象与该一次函数的图象交于第二、四象限内的 A,B 两点.
的图象与该一次函数的图象交于第二、四象限内的 A,B 两点.
(1)求该一次函数的解析式;
(2)若 AC=2BC,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
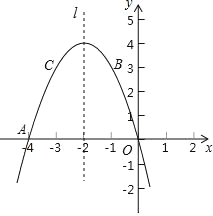
【题目】如图,已知二次函数 y=ax2+bx+c 的图象经过点 A(﹣4,0),B(﹣1,3),C(﹣3,3).
(1)求此二次函数的解析式
(2)设此二次函数的对称轴为直线 l,该图象上的点 P(m,n)在第三象限, 其关于直线 1 的对称点为 M,点 M 关于 y 轴的对称点为 N,若四边形 OAPN 的面积为 20,求 m,n 的值;
(3)在对称轴直线 l 上是否存在一点 D,使△ADC 的周长最短,如果存在,求出点 D 的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上老师提出了如下问题:
尺规作图:作![]() 中
中![]() 边上的高线
边上的高线
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
作法:如图,
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)小乐和小马帮助小东完成下面的证明.
小乐:证明:![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上(依据1).
的垂直平分线上(依据1).
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() 线段
线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
小乐:证明:![]() ,
,![]() ,
,![]()
![]()
![]()
又![]()
![]() (依据2)
(依据2)
∴线段![]() 是
是![]() 中
中![]() 边上的高线
边上的高线
上述证明过程中的“依据1”和“依据2”分别指什么?
(3)请你用不同于小东的方法完成老师提出的问题.
(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 边上的高
边上的高![]() 的长度为__________.
的长度为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com