
ЁОЬтФПЁПЪ§бЇПЮЩЯРЯЪІЬсГіСЫШчЯТЮЪЬтЃК
ГпЙцзїЭМЃКзї![]() жа
жа![]() БпЩЯЕФИпЯп
БпЩЯЕФИпЯп
вбжЊЃК![]() ЃЎ
ЃЎ
ЧѓзїЃК![]() жа
жа![]() БпЩЯЕФИпЯп
БпЩЯЕФИпЯп![]() ЃЎ
ЃЎ
ЯТУцЪЧаЁЖЋЩшМЦЕФЁАзї![]() жа
жа![]() БпЩЯЕФИпЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
БпЩЯЕФИпЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
зїЗЈЃКШчЭМЃЌ
ЂйвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЕФГЄЮЊАыОЖзїЛЁЃЌвдЕу
ЕФГЄЮЊАыОЖзїЛЁЃЌвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁдк
ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁдк![]() ЯТЗННЛгкЕу
ЯТЗННЛгкЕу![]() ЃЛ
ЃЛ
ЂкСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЫљвдЯпЖЮ![]() ЪЧ
ЪЧ![]() жа
жа![]() БпЩЯЕФИпЯпЃЎ
БпЩЯЕФИпЯпЃЎ
ИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉаЁРжКЭаЁТэАяжњаЁЖЋЭъГЩЯТУцЕФжЄУїЃЎ
аЁРжЃКжЄУїЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() Еу
Еу![]() ЃЌ
ЃЌ![]() ЗжБ№дкЯпЖЮ
ЗжБ№дкЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЩЯЃЈвРОн1ЃЉЃЎ
ЕФДЙжБЦНЗжЯпЩЯЃЈвРОн1ЃЉЃЎ
![]() ДЙжБЦНЗжЯпЖЮ
ДЙжБЦНЗжЯпЖЮ![]() ЃЎ
ЃЎ
![]() ЯпЖЮ
ЯпЖЮ![]() ЪЧ
ЪЧ![]() жа
жа![]() БпЩЯЕФИпЯпЃЎ
БпЩЯЕФИпЯпЃЎ
аЁРжЃКжЄУїЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]()
![]()
гж![]()
![]() ЃЈвРОн2ЃЉ
ЃЈвРОн2ЃЉ
ЁрЯпЖЮ![]() ЪЧ
ЪЧ![]() жа
жа![]() БпЩЯЕФИпЯп
БпЩЯЕФИпЯп
ЩЯЪіжЄУїЙ§ГЬжаЕФЁАвРОн1ЁБКЭЁАвРОн2ЁБЗжБ№жИЪВУД?
ЃЈ3ЃЉЧыФугУВЛЭЌгкаЁЖЋЕФЗНЗЈЭъГЩРЯЪІЬсГіЕФЮЪЬтЃЎ
ЃЈ4ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() БпЩЯЕФИп
БпЩЯЕФИп![]() ЕФГЄЖШЮЊ__________ЃЎ
ЕФГЄЖШЮЊ__________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉвРОн1ЃКЕНЯпЖЮСНИіЖЫЕуОрРыЯрЕШЕФЕудкЯпЖЮЕФДЙжБЦНЗжЯпЩЯЃЛвРОн2ЃКШ§ЯпКЯвЛЃЛЃЈ3ЃЉЯъМћНтЮіЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвЊЧѓЛГіЭМаЮМДПЩЃЛ
ЃЈ2ЃЉИљОнЯпЖЮЕФДЙжБЦНЗжЯпЕФХаЖЈКЭЕШбќШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬт
ЃЈ3ЃЉПЩвдЯШЙЙдьвЛИіЕШбќШ§НЧаЮШЛКѓРћгУДЙжБЦНЗжЯпЕФХаЖЈзїГіИпЯп
ЃЈ4ЃЉРћгУ30ЁуЕФЬиЪтаджЪМАЙДЙЩЖЈРэМДПЩЧѓГіД№АИ
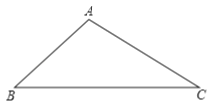
НтЃКЃЈ1ЃЉЭМаЮШчЭМЫљЪОЃК
ЃЈ2ЃЉвРОн1ЃКЕНЯпЖЮСНИіЖЫЕуОрРыЯрЕШЕФЕудкЯпЖЮЕФДЙжБЦНЗжЯпЩЯ
вРОн2ЃКШ§ЯпКЯвЛ
ЃЈ3ЃЉШчЭМЫљЪО
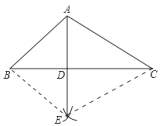
Ђйвд![]() ЮЊдВаФ
ЮЊдВаФ![]() ГЄЮЊАыОЖдк
ГЄЮЊАыОЖдк![]() ЩЯНиШЁ
ЩЯНиШЁ![]()
ЂквдШЮвтГЄЮЊАыОЖЗжБ№вд![]() ЁЂ
ЁЂ![]() ЮЊдВаФЛЛЁНЛгкЕуE
ЮЊдВаФЛЛЁНЛгкЕуE
ЂлСЌНг![]() НЛ
НЛ![]() гк
гк![]() МДЮЊЫљЧѓ
МДЮЊЫљЧѓ
ЃЈ4ЃЉ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгШШЦјЧђCДІВтЕУЕиУцAЃЌBСНЕуЕФИЉНЧЗжБ№ЮЊ30ЁуЃЌ45ЁуЃЌДЫЪБШШЦјЧђCДІЫљдкЮЛжУЕНЕиУцЩЯЕуAЕФОрРыЮЊ400УзЃЎЧѓЕиУцЩЯAЃЌBСНЕуМфЕФОрРыЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцЕФВФСЯЃЌШЛКѓНтД№ЮЪЬтЃК
ЮвУЧаТЖЈвхвЛжжШ§НЧаЮЃЌСНБпЕФЦНЗНКЭЕШгкЕкШ§БпЦНЗНЕФkБЖЕФШ§НЧаЮНазіЁАkБЖШ§НЧаЮЁБ(kЮЊе§ЪЕЪ§)ЃЎ
ЃЈ1ЃЉРэНтЃКИљОнЁАkБЖШ§НЧаЮЁБЕФЖЈвхЬюПе(ЬюЁАШёНЧЁБЁЂЁАжБНЧЁБЛђЁАЖлНЧЁБ)ЃК
ЂйЕБ![]() ЪБЃЌkБЖШ§НЧаЮвЛЖЈЪЧ_____________Ш§НЧаЮЃЛ
ЪБЃЌkБЖШ§НЧаЮвЛЖЈЪЧ_____________Ш§НЧаЮЃЛ
ЂкЕБ![]() ЪБЃЌkБЖШ§НЧаЮвЛЖЈЪЧ______________Ш§НЧаЮЃЎ
ЪБЃЌkБЖШ§НЧаЮвЛЖЈЪЧ______________Ш§НЧаЮЃЎ
ЃЈ2ЃЉЬНОПЃКЕБ![]() ЪБЃЌвбжЊRtЁїABCЮЊЁАkБЖШ§НЧаЮЁБЃЌЧв
ЪБЃЌвбжЊRtЁїABCЮЊЁАkБЖШ§НЧаЮЁБЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫљгаТњзуЬѕМўЕФkжЕЃЎ
ЃЌЧѓЫљгаТњзуЬѕМўЕФkжЕЃЎ
ЃЈ3ЃЉЭиеЙЃКШєRtЁїABCЪЧЁАkБЖШ§НЧаЮЁБЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .ЕБ
.ЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
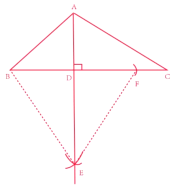
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЪЧЫЋЧњЯп![]() дкЕквЛЯѓЯоЕФЗжжЇЩЯЕФвЛИіЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЫФЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯБфЛЏЃЌЕЋЕуCЪМжедкЕкЫФЯѓЯоЃЌЧвЫЋЧњЯп
дкЕквЛЯѓЯоЕФЗжжЇЩЯЕФвЛИіЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЫФЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯБфЛЏЃЌЕЋЕуCЪМжедкЕкЫФЯѓЯоЃЌЧвЫЋЧњЯп![]() ЪМжеОЙ§ЕуCЃЌдђkЕФжЕЮЊ_____ЃЎ
ЪМжеОЙ§ЕуCЃЌдђkЕФжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїOA1B1ЃЌЁїA1A2B2ЃЌЁїA2A3B3ЃЌЁЃЌЁїAnЉ1AnBnЃЌЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌаББпOB1ЃЌA1B2ЃЌЁЃЌAnЉ1BnЕФжаЕуP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЖМдкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌдђy1+y2+y3+Ё+yn=_____ЃЎ
ЕФЭМЯѓЩЯЃЌдђy1+y2+y3+Ё+yn=_____ЃЎ
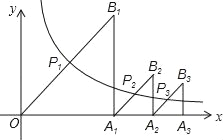
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
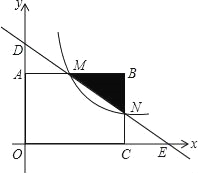
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуOгызјБъдЕужиКЯЃЌЖЅЕуAЃЌCЗжБ№дкзјБъжсЩЯЃЌЖЅЕуBЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌЙ§ЕуDЃЈ0ЃЌ3ЃЉКЭEЃЈ6ЃЌ0ЃЉЕФжБЯпЗжБ№гыABЃЌBCНЛгкЕуMЃЌNЃЎ
ЃЈ1ЃЉЧѓжБЯпDEЕФНтЮіЪНКЭЕуMЕФзјБъЃЛ
ЃЈ2ЃЉШєЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуMЃЌдкИУЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPMNЕФУцЛ§ЕШгкЁїOMNЕФУцЛ§ЕФвЛАыЃЌШєДцдкЃЌЧѓЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуMЃЌдкИУЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPMNЕФУцЛ§ЕШгкЁїOMNЕФУцЛ§ЕФвЛАыЃЌШєДцдкЃЌЧѓЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыЁїMNBгаЙЋЙВЕуЃЌЧыжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгыЁїMNBгаЙЋЙВЕуЃЌЧыжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙужнЛ№ГЕФЯеОЙуГЁМЦЛЎдкЙуГЁФкжжжВAЃЌBСНжжЛЈФОЙВ 6600ПУЃЌШєAЛЈФОЪ§СПЪЧBЛЈФОЪ§СПЕФ2БЖЩй600ПУЃЎ
ЃЈ1ЃЉAЃЌBСНжжЛЈФОЕФЪ§СПЗжБ№ЪЧЖрЩйПУЃП
ЃЈ2ЃЉШчЙћдАСжДІАВХХ26ШЫЭЌЪБжжжВетСНжжЛЈФОЃЌУПШЫУПЬьФмжжжВAЛЈФО60ПУЛђBЛЈФО40ПУЃЌгІЗжБ№АВХХЖрЩйШЫжжжВAЛЈФОКЭBЛЈФОЃЌВХФмШЗБЃЭЌЪБЭъГЩИїздЕФШЮЮёЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛЫвДЌЯђе§ББКНааЃЌдкAДІПДЕНЕЦЫўSдкДЌЕФББЦЋЖЋ30ЁуЕФЗНЯђЩЯЃЌКНаа12КЃРяЕНДяBЕуЃЌдкBДІПДЕНЕЦЫўSдкДЌЕФББЦЋЖЋ60ЁуЕФЗНЯђЩЯЃЌДЫДЌМЬајбие§ББЗНЯђКНааЙ§ГЬжаОрЕЦЫўSЕФзюНќОрРыЪЧ_____КЃРяЃЈВЛНќЫЦМЦЫуЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРЃЌШЮвтвЛИіе§ећЪ§nЖМПЩвдНјааетбљЕФЗжНтЃКn=pЁСqЃЈpЃЌqЪЧе§ећЪ§ЃЌЧвpЁмqЃЉЃЌдкnЕФЫљгаетжжЗжНтжаЃЌШчЙћpЃЌqСНвђЪ§жЎВюЕФОјЖджЕзюаЁЃЌЮвУЧОЭГЦpЁСqЪЧnЕФзюМбЗжНтЃЌВЂЙцЖЈЃКFЃЈnЃЉ=![]() ЃЌР§Шч12ПЩвдЗжНтГЩ1ЁС12,2ЁС6Лђ3ЁС4ЃЌвђЮЊ12-1ЃО6-2ЃО4-3ЃЌЫљга3ЁС4ЪЧзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=
ЃЌР§Шч12ПЩвдЗжНтГЩ1ЁС12,2ЁС6Лђ3ЁС4ЃЌвђЮЊ12-1ЃО6-2ЃО4-3ЃЌЫљга3ЁС4ЪЧзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=![]() .
.
ЃЈ1ЃЉШчЙћвЛИіе§ећЪ§aЪЧСэЭтвЛИіе§ећЪ§bЕФЦНЗНЃЌЮвУЧГЦе§ећЪ§aЪЧЭъШЋЦНЗНЪ§ЃЌЧѓжЄЃКЖдШЮвтвЛИіЭъШЋЦНЗНЪ§mЃЌзмгаFЃЈmЃЉ=1.
ЃЈ2ЃЉШчЙћвЛИіСНЮЛе§ећЪ§tЃЌt=10x+yЃЈ1ЁмxЁмyЁм9,x,yЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюЮЊ18ЃЌФЧУДЮвУЧГЦетИіЪ§tЮЊЁАМЊЯщЪ§ЁБЃЌЧѓЫљгаЁАМЊЯщЪ§ЁБжаFЃЈtЃЉЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com