
【题目】 如图,在边长为4的正方形纸片ABCD中,从边CD上剪去一个矩形EFGH,且有EF=DH=CE=1cm,FG=2cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止.以AP为边在AP的下方做正方形AQKP,设点P运动时间为t(s),正方形AQKP和纸片重叠部分的面积为S(cm2),则S与t之间的函数关系用图象表示大致是( )
A. 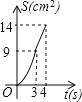 B.
B. 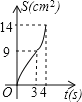
C. 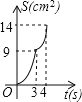 D.
D. 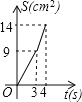
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,位于中国广东省伶仃洋区域内,为珠江三角洲地区环线高速公路南环段,青州航道桥“中国结三地同心”主题的斜拉索塔如图(1)所示.某数学兴趣小组根据材料编制了如下数学问题,请你解答.
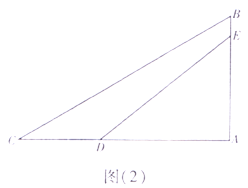
如图(2),BC,DE为主塔AB(主塔AB与桥面AC垂直)上的两条钢索,桥面上C、D两点间的距离为16m,主塔上A、E两点的距离为18.4m,已知BC与桥面AC的夹角为30°,DE与桥面AC的夹角为38°。求主塔AB的高.(结果精确到1米,参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
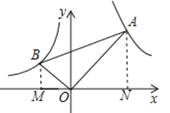
【题目】如图,在![]() 轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数
轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数![]() ,
,![]() 的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
A. 逐渐变小B. 逐渐变大C. 时大时小D. 保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,![]() 地到宁波港的路程比原来缩短了
地到宁波港的路程比原来缩短了![]() .已知运输车速度不变时,行驶时间将从原来的
.已知运输车速度不变时,行驶时间将从原来的![]() 缩短到
缩短到![]() .
.
(1)求![]() 地经杭州湾跨海大桥到宁波港的路程.
地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从![]() 地到宁波港的运输成本是每千米
地到宁波港的运输成本是每千米![]() 元,时间成本是每时
元,时间成本是每时![]() 元,那么该车货物从
元,那么该车货物从![]() 地经杭州湾跨海大桥到宁波港的运输费用是多少元?
地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从![]() 地经杭州湾跨海大桥到宁波港,再从宁波港运到
地经杭州湾跨海大桥到宁波港,再从宁波港运到![]() 地.若有一批货物(不超过
地.若有一批货物(不超过![]() 车)从
车)从![]() 地按外运路线运到
地按外运路线运到![]() 地的运费需
地的运费需![]() 元,其中从
元,其中从![]() 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到
地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到![]() 地的海上运费对一批不超过
地的海上运费对一批不超过![]() 车的货物计费方式是:
车的货物计费方式是:![]() 车
车![]() 元,当货物每增加
元,当货物每增加![]() 车时,每车的海上运费就减少
车时,每车的海上运费就减少![]() 元,问这批货物有几车?
元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(20,19)表示的正整数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
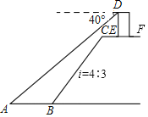
【题目】如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=4,BC=2,点D在射线AB上,在构成的图形中,△ACD为等腰三角形,且存在两个互为相似的三角形,则CD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com