
【题目】如图,在![]() 轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数
轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数![]() ,
,![]() 的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
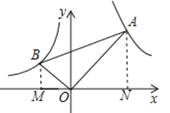
A. 逐渐变小B. 逐渐变大C. 时大时小D. 保持不变
【答案】D
【解析】
如图,作辅助线;首先证明△BOM∽△OAN,得到![]() ;设B(m,
;设B(m,![]() ),A(n,
),A(n,![]() ),得到BM=
),得到BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,进而得到mn=2,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=
,OM=m,ON=n,进而得到mn=2,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=![]() ,为定值,即可解决问题.
,为定值,即可解决问题.
解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴![]() ;
;
设B(m,![]() ),A(n,
),A(n,![]() ),
),
则BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,
,OM=m,ON=n,
∴mn=![]() ,mn=2;
,mn=2;
∵∠AOB=90°,
∴tan∠OAB=![]() ①;
①;
∵△BOM∽△OAN,
∴![]() ②,
②,
由①②知tan∠OAB=![]() 为定值,
为定值,
∴∠OAB的大小不变,
故选:D.


科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
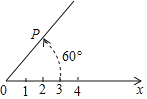
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;
(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
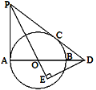
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=3,tan∠PDA=![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见.如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠BOD=45°,当将遮阳伞撑开至OE位置时,测得∠BOE=60°,且此时遮阳伞边沿上升的竖直高度BC为30cm,求当遮阳伞撑开至OE位置时,伞下半径EC的长.(结果保留根号).
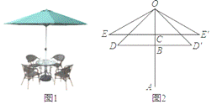
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
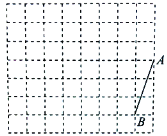
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0; (2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1; (4)(x+3)2=(1﹣2x)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在边长为4的正方形纸片ABCD中,从边CD上剪去一个矩形EFGH,且有EF=DH=CE=1cm,FG=2cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止.以AP为边在AP的下方做正方形AQKP,设点P运动时间为t(s),正方形AQKP和纸片重叠部分的面积为S(cm2),则S与t之间的函数关系用图象表示大致是( )
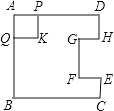
A. 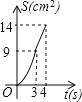 B.
B. 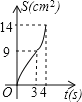
C. 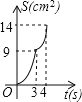 D.
D. 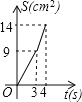
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5,tanD=![]() ,点E在BC上运动(不与B,C重合),将四边形AECD沿直线AE翻折后,点C落在C′处,点D′落在D处,C′D′与AB交于点F,当C′D'⊥AB时,CE长为_____.
,点E在BC上运动(不与B,C重合),将四边形AECD沿直线AE翻折后,点C落在C′处,点D′落在D处,C′D′与AB交于点F,当C′D'⊥AB时,CE长为_____.
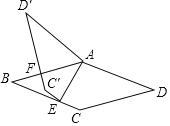
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com