
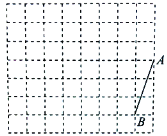
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】问题情填,
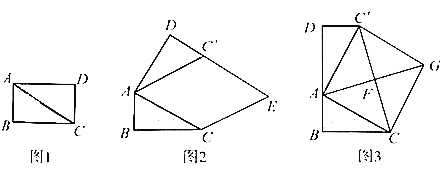
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
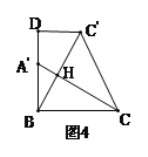
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;
(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?
查看答案和解析>>
科目:初中数学 来源: 题型:
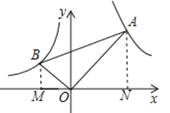
【题目】如图,在![]() 轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数
轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别于函数![]() ,
,![]() 的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
的图像交于B、A两点,则∠OAB大小的变化趋势为 ( )
A. 逐渐变小B. 逐渐变大C. 时大时小D. 保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
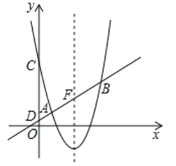
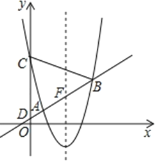
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于A(1,1),B两点,与
交于A(1,1),B两点,与![]() 轴交于点C,直线
轴交于点C,直线![]() 与轴交于点D.
与轴交于点D.
(1)求抛物线的对称轴和点C的坐标;
(2)若在![]() 轴上有且只有一点P,使∠APB=90°,求
轴上有且只有一点P,使∠APB=90°,求![]() 的值;
的值;
(3)设直线![]() 与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若
与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD的面积相等,求点G的坐标.
,且△BCG与△BCD的面积相等,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,![]() 地到宁波港的路程比原来缩短了
地到宁波港的路程比原来缩短了![]() .已知运输车速度不变时,行驶时间将从原来的
.已知运输车速度不变时,行驶时间将从原来的![]() 缩短到
缩短到![]() .
.
(1)求![]() 地经杭州湾跨海大桥到宁波港的路程.
地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从![]() 地到宁波港的运输成本是每千米
地到宁波港的运输成本是每千米![]() 元,时间成本是每时
元,时间成本是每时![]() 元,那么该车货物从
元,那么该车货物从![]() 地经杭州湾跨海大桥到宁波港的运输费用是多少元?
地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从![]() 地经杭州湾跨海大桥到宁波港,再从宁波港运到
地经杭州湾跨海大桥到宁波港,再从宁波港运到![]() 地.若有一批货物(不超过
地.若有一批货物(不超过![]() 车)从
车)从![]() 地按外运路线运到
地按外运路线运到![]() 地的运费需
地的运费需![]() 元,其中从
元,其中从![]() 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到
地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到![]() 地的海上运费对一批不超过
地的海上运费对一批不超过![]() 车的货物计费方式是:
车的货物计费方式是:![]() 车
车![]() 元,当货物每增加
元,当货物每增加![]() 车时,每车的海上运费就减少
车时,每车的海上运费就减少![]() 元,问这批货物有几车?
元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
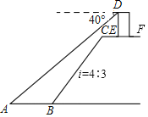
【题目】如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
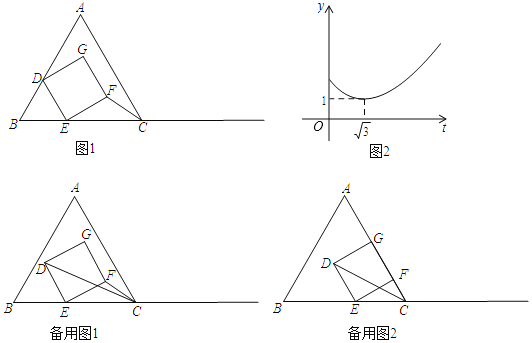
【题目】等边△ABC与正方形DEFG如图1放置,其中D,E两点分别在AB,BC上,且BD=BE.
(1)求∠DEB的度数;
(2)当正方形DEFG沿着射线BC方向以每秒1个单位长度的速度平移时,CF的长度y随着运动时间变化的函数图象如图2所示,且当t=![]() 时,y有最小值1;
时,y有最小值1;
①求等边△ABC的边长;
②连结CD,在平移的过程中,求当△CEF与△CDE同时为等腰三角形时t的值;
③从平移运动开始,到GF恰落在AC边上时,请直接写出△CEF外接圆圆心的运动路径的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com