
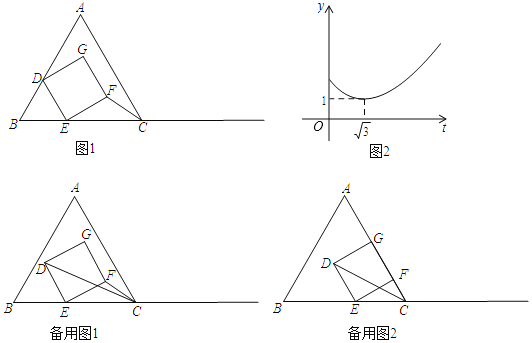
����Ŀ���ȱߡ�ABC��������DEFG��ͼ1���ã�����D��E����ֱ���AB��BC�ϣ���BD��BE��
��1�����DEB�Ķ�����
��2����������DEFG��������BC������ÿ��1����λ���ȵ��ٶ�ƽ��ʱ��CF�ij���y�����˶�ʱ��仯�ĺ���ͼ����ͼ2��ʾ���ҵ�t=![]() ʱ��y����Сֵ1��
ʱ��y����Сֵ1��
����ȱߡ�ABC�ı߳���
������CD����ƽ�ƵĹ����У���CEF���CDEͬʱΪ����������ʱt��ֵ��
����ƽ���˶���ʼ����GFǡ����AC����ʱ����ֱ��д����CEF���ԲԲ�ĵ��˶�·���ij��ȣ�
���𰸡���1����BED��60�㣻��2����2+2![]() ����t��2
����t��2![]() ��2��2+2
��2��2+2![]() ����
����![]() ��
��
��������
��1��֤����BDE�ǵȱ������μ��ɽ�����⣮
��2������ͼ2�У�������DEFGƽ�ƹ����У�FF���BC����֤�ı���EFF��E����ƽ���ı��Σ������⣬��CF���BCʱ��CF���ֵ��С����ʱCF�䣽1����ֱ�����������E��F�䣬CE�伴�ɣ�
�����������ηֱ�ͼ����⼴�ɣ�
����ͼ5�У����CE��F������Բ��Բ��ΪI������IE�䣬CI��IF�䣬��ֱ��FF�佻AC��H����CB��ȡһ��J��ʹ��CH��CJ������JH��IJ��֤����HCF��ա�JCI��SAS�����Ƴ�JI��HF�䣬���ɽ�����⣮
�⣺��1����ͼ1�У�

�ߡ�ABC�ǵȱ������Σ�
���B��60�㣬
��BD��BE��
���BDE�ǵȱ������Σ�
���BED��60�㣮
��2������ͼ2�У�

��ͼ������DEFGƽ�ƹ����У�FF���BC����֤�ı���EFF��E����ƽ���ı��Σ�
�����⣬��CF���BCʱ��CF���ֵ��С����ʱCF�䣽1��
��Rt��CE��F���У��ߡ�E��CF�䣽90�㣬��F��E��C��30�㣬CF�䣽1��
��EF��E��F�䣽2��CE�䣽![]() ��
��
��t��EE�䣽![]() ��
��
��EE�䣽CE�䣽![]() ��
��
��BE��DE��EF��2��
��BC��BE+EE��+CE�䣽2+2![]() ��
��
����ͼ3�У���E��D�䣽E��F�䣽CE�䣽2ʱ����CEF���CDEͬʱΪ���������Σ���ʱt��EE�䣽BC��BE��CE�䣽2+2![]() ��4��2
��4��2![]() ��2��
��2��

��ͼ4�У���E��C��E��D�䣽E��F�䣽2ʱ����CEF���CDEͬʱΪ���������Σ���ʱt��EE�䣽BC+CE�䩁BE��BC��2+2![]() ��
��

����������t��2![]() ��2��2+2
��2��2+2![]() ʱ����CEF���CDEͬʱΪ���������Σ�
ʱ����CEF���CDEͬʱΪ���������Σ�
����ͼ5�У����CE��F������Բ��Բ��ΪI������IE�䣬CI��IF�䣬��ֱ��FF�佻AC��H����CB��ȡһ��J��ʹ��CH��CJ������JH��IJ��

��IE�䣽IF�䣽IC��
���F��E��C��![]() ��F��IC��
��F��IC��
�ߡ�F��E��C��30�㣬
���CJF�䣽60�㣬
���CIF���ǵȱ������Σ�
��CH��CJ����HCJ��60�㣬
���HCJ�ǵȱ������Σ�
��CH��CJ��CF�䣽CI����HCJ����F��CI��60�㣬
���HCF�䣽��JCI��
���HCF��ա�JCI��SAS����
��F��H��IJ����CHF�䣽��CJI��120�㣬
���I���˶��켣���߶Σ���JI��HF�䣬
������֪FH��![]() ��
��
���CEF���ԲԲ�ĵ��˶�·���ij���Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
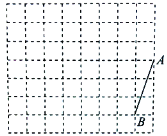
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�Ķ˵����С�����εĶ����ϣ�
��1����ͼ�л������߶�ABΪһ�ߵľ���ABCD�����������Σ����ҵ�C�͵�D����С�����εĶ����ϣ�
��2����ͼ�л������߶�ABΪһ�����ױ߳�Ϊ![]() �ĵ���������ABE����E��С�����εĶ��㣬��CE= ��
�ĵ���������ABE����E��С�����εĶ��㣬��CE= ��
��3��F�DZ�AD��һ���㣬��CF+EF����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
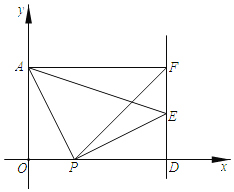
����Ŀ����ƽ��ֱ������ϵ�У���A����Ϊ(0��3)��x���ϵ�P(t��0)�����߶�AP�Ƶ�P˳ʱ����ת90��õ�PE������E��ֱ��l��x����D������A��AF��ֱ��l��F��
(1)����E��DF���е�ʱ����ֱ��PE�ĺ�������ʽ��
(2)��t��5ʱ�����PEF�������
(3)��ֱ��l���Ƿ���ڵ�G��ʹ�á�APO����PFD+��PGD�������ڣ�����t�Ĵ���ʽ��ʾ��G�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ţ�������ǰ���֪���ط�С�ԣ�ij�ֵ꾭�����֣���ÿ��ţ�������ۼ�Ϊ6Ԫʱ��ÿ��������500�룻��ÿ��ţ�������ۼ�ÿ����0.5Ԫʱ��ÿ��ͻ�������20�룬��ÿ��ţ�������ۼ�����![]() Ԫʱ��һ���Ӫҵ��Ϊ
Ԫʱ��һ���Ӫҵ��Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() �ĺ�����ϵʽ����Ҫ��д��
�ĺ�����ϵʽ����Ҫ��д��![]() ��ȡֵ��Χ����
��ȡֵ��Χ����
��2�����ǵ��˿Ϳɽ��ܼ۸�![]() Ԫ/��ķ�Χ��
Ԫ/��ķ�Χ��![]() ����
����![]() Ϊ�������������������أ���÷ֵ��ţ����ÿ�����Ԫʱ��ÿ���ţ����Ӫҵ��������Ӫҵ���Ƕ���Ԫ��
Ϊ�������������������أ���÷ֵ��ţ����ÿ�����Ԫʱ��ÿ���ţ����Ӫҵ��������Ӫҵ���Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
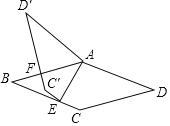
����Ŀ����ͼ��������ABCD�У�AB��5��tanD��![]() ����E��BC���˶�������B��C�غϣ������ı���AECD��ֱ��AE���ۺ�C����C�䴦����D������D����C��D����AB���ڵ�F����C��D'��ABʱ��CE��Ϊ_____��
����E��BC���˶�������B��C�غϣ������ı���AECD��ֱ��AE���ۺ�C����C�䴦����D������D����C��D����AB���ڵ�F����C��D'��ABʱ��CE��Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ס�������ũ����ij��ƣ��о���Ա�ֱ��ȡ��6���磬������ǵĸ߶ȣ���λ��cm�����£�
�ף�98��102��100��100��101��99���ң�100��103��101��97��100��99��
��1������Ϊ����ũ���ﳤ�ø�һЩ��˵�����ɣ�
��2������Ϊ����ũ���ﳤ�ø�����һЩ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
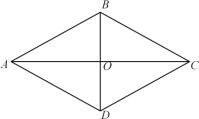
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC��BD��ACƽ�֡�BAD��
��1�����������ĸ���������AB��AD����OB��OD���ۡ�ACB����ACD����AD��BC�������ĸ������У�ѡ��һ�����ʵ�������ʹ�ı���ABCD�����Σ���������ǣ���д��ţ���
��2��������ѡ���������֤���ı���ABCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ��չ�ԡ�����ϲ����ְҵ��Ϊ����ĵ�����Χ�ơ�����Ա����ʦ��ҽ������ʦ������Ա������ְҵ�У�����ϲ����һ�ࣿ����ѡ��ֻѡһ�ࣩ�������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ���������ͼ���ṩ����Ϣ�ش��������⣺
��1�����ε��鹲��ȡ�˶�����ѧ����
��2�����ڱ������ѧ���У���ϲ����ʦְҵ������������ȫ����ͳ��ͼ��
��3����������ѧ����1500��ѧ����������Ƹ���ѧ��ϲ����ʦְҵ��ѧ���ж�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=-x2+4x-1��y�ύ�ڵ�C��CD��x�ύ����������һ��D��AB��x�ύ�������ڵ�A��B����A�ڵ�B����࣬��������ڵ�һ���ޣ�BH��CD�ڵ�H�����A�ĺ�����Ϊm��
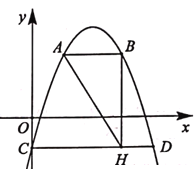
��1����m=1ʱ����AB�ij�.
��2����AH=![]() ��CH-DH������m��ֵ.
��CH-DH������m��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com