
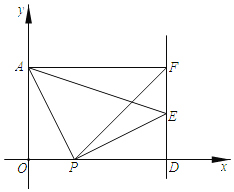
【题目】在平面直角坐标系中,点A坐标为(0,3),x轴上点P(t,0),将线段AP绕点P顺时针旋转90°得到PE,过点E作直线l⊥x轴于D,过点A作AF⊥直线l于F.
(1)当点E是DF的中点时,求直线PE的函数表达式.
(2)当t=5时,求△PEF的面积.
(3)在直线l上是否存在点G,使得∠APO=∠PFD+∠PGD?若存在,试用t的代数式表示点G的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)17;(3)G(3+t,﹣
;(2)17;(3)G(3+t,﹣![]() ).
).
【解析】
(1)证明Rt△APO≌Rt△PED(HL),得到ED=![]() =PO,DO=OP+PD=OP+AO=3+
=PO,DO=OP+PD=OP+AO=3+![]() =
=![]() ,求出点E(
,求出点E(![]() ,
,![]() ),P(
),P(![]() ,0),将点代入解析式即可求解;
,0),将点代入解析式即可求解;
(2)由(1)的全等可得到OD=8,DF=3,所以S△APE=5×8-![]() ×3×5×2-
×3×5×2-![]() ×2×8=17;
×2×8=17;
(3)假设在直线l上是否存在点G,使得∠APO=∠PFD+∠PGD,可以得到A,P,E,F四点共圆,所以∠PAE=∠PFE=45°,PD=FE=3,FP=3![]() ,
,
设E(m,n),由AP⊥PE,![]() ,再由等腰直角三角形PDF可得PD=3,D(3+t,0),E(3+t,t)可以证明△APF∽△PGF,所以
,再由等腰直角三角形PDF可得PD=3,D(3+t,0),E(3+t,t)可以证明△APF∽△PGF,所以![]() ,即18=(3+t)(3+DG),得到DG=
,即18=(3+t)(3+DG),得到DG=![]() ,进而取得G点坐标.
,进而取得G点坐标.
(1)∵线段AP绕点P顺时针旋转90°得到PE,
∴AP=PE,∠APE=90°,
∵∠APO+∠PED=∠APO+∠OAP=90°,
∴∠PED=∠APO,
∴Rt△APO≌Rt△PED(HL),
∴OP=ED,AO=PD,
∵OA=3,点E是DF的中点,
∴ED=![]() =PO,
=PO,
∴DO=OP+PD=OP+AO=3+![]() =
=![]() ,
,
∴E(![]() ,
,![]() ),P(
),P(![]() ,0)
,0)
设直线PE的解析式为y=kx+b,
∴ ,
,
∴ ,
,
∴y=![]() ;
;
(2)∵Rt△APO≌Rt△PED,
∴OP=ED,AO=PD,
∵OA=5,OP=3,
∴OD=8,DF=3,
∴S△APE=5×8﹣![]() ×3×5×2﹣
×3×5×2﹣![]() ×8=17;
×8=17;
(3)假设在直线l上是否存在点G,使得∠APO=∠PFD+∠PGD,
∵AP⊥PE,AF⊥FE,
∴A,P,E,F四点共圆,
∴∠PAE=∠PFE=45°,
∴∠APF=∠PGD,
∴PD=FE=3,
∴FP=3![]() ,
,
设E(m,n),
∵AP⊥PE,
∴![]() ,
,
∵PD=3,
∴D(3+t,0),
∴m=3+t,
∴n=t,
∴E(3+t,t)
∴△APF∽△PGF,
∴![]() ,
,
∴18=(3+t)(3+DG),
∴DG=![]() ,
,
∴G(3+t,﹣![]() );
);



 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,![]() 地到宁波港的路程比原来缩短了
地到宁波港的路程比原来缩短了![]() .已知运输车速度不变时,行驶时间将从原来的
.已知运输车速度不变时,行驶时间将从原来的![]() 缩短到
缩短到![]() .
.
(1)求![]() 地经杭州湾跨海大桥到宁波港的路程.
地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从![]() 地到宁波港的运输成本是每千米
地到宁波港的运输成本是每千米![]() 元,时间成本是每时
元,时间成本是每时![]() 元,那么该车货物从
元,那么该车货物从![]() 地经杭州湾跨海大桥到宁波港的运输费用是多少元?
地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从![]() 地经杭州湾跨海大桥到宁波港,再从宁波港运到
地经杭州湾跨海大桥到宁波港,再从宁波港运到![]() 地.若有一批货物(不超过
地.若有一批货物(不超过![]() 车)从
车)从![]() 地按外运路线运到
地按外运路线运到![]() 地的运费需
地的运费需![]() 元,其中从
元,其中从![]() 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到
地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到![]() 地的海上运费对一批不超过
地的海上运费对一批不超过![]() 车的货物计费方式是:
车的货物计费方式是:![]() 车
车![]() 元,当货物每增加
元,当货物每增加![]() 车时,每车的海上运费就减少
车时,每车的海上运费就减少![]() 元,问这批货物有几车?
元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
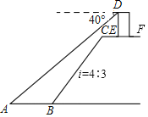
【题目】如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=4,BC=2,点D在射线AB上,在构成的图形中,△ACD为等腰三角形,且存在两个互为相似的三角形,则CD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
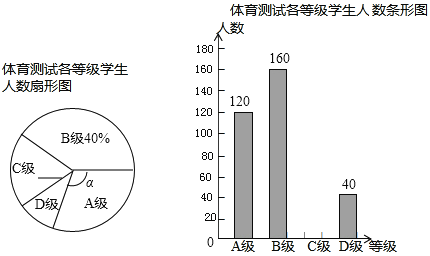
【题目】2018年某市学业水平体育测试即将举行,某校为了解同学们的训练情况,从九年级学生中随机抽取部分学生进行了体育测试(把成绩分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)求本次抽测的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)在测试中甲乙、丙、丁四名同学表现非常优秀,现决定从这四名同学中任选两名给大家介绍训练经验,求恰好选中甲、乙两名同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
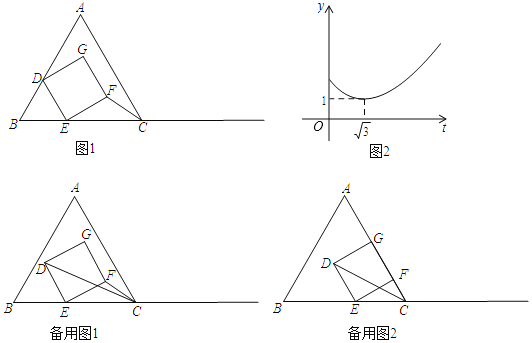
【题目】等边△ABC与正方形DEFG如图1放置,其中D,E两点分别在AB,BC上,且BD=BE.
(1)求∠DEB的度数;
(2)当正方形DEFG沿着射线BC方向以每秒1个单位长度的速度平移时,CF的长度y随着运动时间变化的函数图象如图2所示,且当t=![]() 时,y有最小值1;
时,y有最小值1;
①求等边△ABC的边长;
②连结CD,在平移的过程中,求当△CEF与△CDE同时为等腰三角形时t的值;
③从平移运动开始,到GF恰落在AC边上时,请直接写出△CEF外接圆圆心的运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
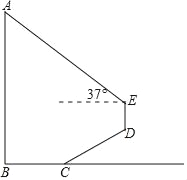
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com