
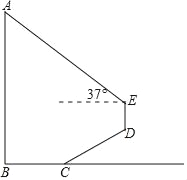
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
【答案】(1)点D的铅垂高度是![]() 米(2)旗杆AB的高度约为7.7米
米(2)旗杆AB的高度约为7.7米
【解析】试题分析:(1)延长ED交射线BC于点H,根据坡度为1:![]() ,可得∠DCH =30°,由直角三角形中30°角所对的边等于斜边的一半,得DH=
,可得∠DCH =30°,由直角三角形中30°角所对的边等于斜边的一半,得DH=![]() ;
;
(2)求出EF和FB的值,在Rt△AEF中,由正切求得AF的值,即可求得AB的值.
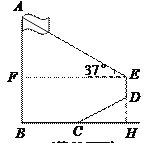
试题解析:(1)延长ED交射线BC于点H.由题意得DH⊥BC.
在Rt△CDH中,∠DHC=90°,tan∠DCH=![]() .
.
∴ ∠DCH=30°.
∴ CD=2DH.
∵ CD=![]() ,
,
∴ DH=![]() ,CH=3 .
,CH=3 .
答:点D的铅垂高度是![]() 米.
米.
(2)过点E作EF⊥AB于F.
由题意得,∠AEF即为点E观察点A时的仰角,
∴ ∠AEF=37°.
∵ EF⊥AB,AB⊥BC,ED⊥BC,
∴ ∠BFE=∠B=∠BHE=90°.
∴ 四边形FBHE为矩形.
∴ EF=BH=BC+CH=6.
FB=EH=ED+DH=1.5+![]() .
.
在Rt△AEF中,∠AFE=90°,AF=EF·tan∠AEF≈6×0.75≈4.5.
∴ AB=AF+FB=6+![]() ≈6+1.73≈7.7.
≈6+1.73≈7.7.
答:旗杆AB的高度约为7.7米.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.在直角三角形中,两条边的平方和等于第三边的平方
B.如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a2+b2=c2,则∠A=90°
D.在△ABC中,若a=3,b=4,则c=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值及点B的坐标;
(2)求△ABC的面积;
(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.
(1)求甲、乙每天能生产多少万只口罩?
(2)问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
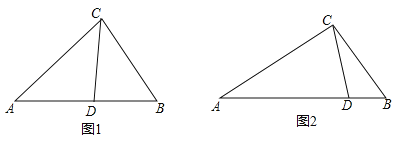
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com