
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



【答案】(1)详见解析;(2)![]() ;(3)当△EFD为等腰三角形时,FG的长度是:
;(3)当△EFD为等腰三角形时,FG的长度是: ![]() .
.
【解析】试题分析:(1)由等边对等角得∠B=∠BED,由同角的余角相等可得∠A=∠GEF,进而由两角分别相等的两个三角形相似,可证△EFG∽△AEG;
(2)作EH⊥AF于点H,由tanA=![]() 及△EFG∽△AEG,得AG=4x,AF=3x,EH=
及△EFG∽△AEG,得AG=4x,AF=3x,EH= ![]() ,
,
可得y关于x的解析式;
(3)△EFD是等腰三角形,分三种情况讨论:①EF=ED;②ED=FD;③ED=EF三种情况讨论即可.
试题解析:(1)∵ ED=BD,
∴ ∠B=∠BED.
∵ ∠ACB=90°,
∴ ∠B+∠A=90°.
∵ EF⊥AB,
∴ ∠BEF=90°.
∴ ∠BED+∠GEF=90°.
∴ ∠A=∠GEF.
∵ ∠G是公共角,
∴ △EFG∽△AEG;
(2)作EH⊥AF于点H.
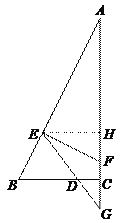
∵ 在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴tanA=![]() =
=![]() ,
,
∴ 在Rt△AEF中,∠AEF=90°,tanA=![]() =
=![]() ,
,
∵ △EFG∽△AEG,
∴![]() ,
,
∵ FG=x,
∴ EG=2x,AG=4x.
∴ AF=3x.
∵ EH⊥AF,
∴ ∠AHE=∠EHF=90°.
∴ ∠EFA+∠FEH=90°.
∵ ∠AEF=90°,
∴ ∠A+∠EFA=90°,
∴ ∠A=∠FEH,
∴ tanA =tan∠FEH,
∴ 在Rt△EHF中,∠EHF=90°,tan∠FEH=![]() =
=![]() ,
,
∴ EH=2HF,
∵ 在Rt△AEH中,∠AHE=90°,tanA=![]() =
=![]() ,
,
∴ AH=2EH,
∴ AH=4HF,
∴ AF=5HF,
∴ HF= ![]() ,
,
∴EH= ![]() ,
,
∴y=![]() FG·EH=
FG·EH=![]() x·
x·![]() =
=![]() 定义域:(0<x≤
定义域:(0<x≤![]() );
);
(3)当△EFD为等腰三角形时,

①当ED=EF时,则有∠EDF=∠EFD,
∵∠BED=∠EFH,
∴∠BEH=∠AHG,
∵∠ACB=∠AEH=90°,
∴∠CEF=∠HEF,即EF为∠GEH的平分线,
则ED=EF=x,DG=8x,
∵anA=![]() ,
,
∴x=3,即BE=3;
②若FE=FD, 此时FG的长度是![]() ;
;
③若DE=DF, 此时FG的长度是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为边在△ABC外作正△ACD,连接BD.
(1)以点A为中心,把△ADB顺时针旋转60°,画出旋转后的图形(保留作图痕迹);
(2)若∠ABC=30°,BC=4,BD=6,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
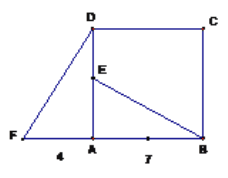
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7.
(1)旋转中心是点 ,旋转了 度,DE的长度是 ;
(2)BE与DF的关系如何? 请说明理由.(提示:延长BE交DF于点G)
查看答案和解析>>
科目:初中数学 来源: 题型:
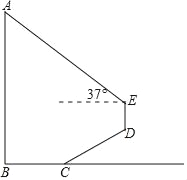
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要生产若干件新产品,需要加工后才能投放市场.现有红星和巨星两个工厂都想加工这批产品,已知红星厂单独加工这批产品比巨星厂单独加工多用20天,红星厂每天可以加工16个,巨星厂每天可以加工24个.公司需付红星厂每天加工费80元,巨星厂每天加工费120元.
(1)这家公司要生产多少件新产品?
(2)公司制定产品加工方案如下:可由每个厂家单独完成,也可由两个厂共同合作完成.在加工过程中,公司需派一名工程师每天到厂家进行技术指导,并负担每天的补助费5元.请你帮公司选择一种既省钱又省时的加工方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题解决)已知点![]() 在
在![]() 内,过点
内,过点![]() 分别作关于
分别作关于![]() 、
、![]() 的对称点
的对称点![]() 、
、![]() .
.
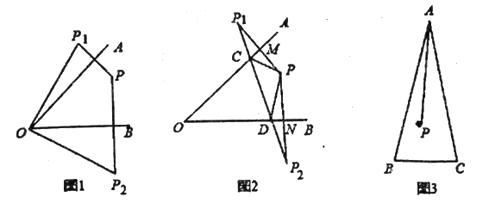
①如图1,若![]() ,请直接写出
,请直接写出![]() ______;
______;
②如图2,连接![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③在②的条件下,若![]() 度(
度(![]() ),请直接写出
),请直接写出![]() ______度(用含
______度(用含![]() 的代数式表示).
的代数式表示).
(2)(拓展延伸)利用“有一个角是![]() 的等腰三角形是等边三角形”这个结论,解答问题:如图3,在
的等腰三角形是等边三角形”这个结论,解答问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内部一定点,
内部一定点,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,请你在图3中画出使
上,请你在图3中画出使![]() 周长最小的点
周长最小的点![]() 、
、![]() 的位置(不写画法),并直接写出
的位置(不写画法),并直接写出![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A.C分别在x轴、y轴上,CB∥OA,OA=8,若点B的坐标为![]() .
.

(1)直接写出点A,C的坐标;
(2)动点P从原点O出发沿x轴以每秒2个单位的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分时停止运动,求P点运动时间;
(3)在(2)的条件下,点P停止运动时,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,AF平分∠BAD交BC于点E,交DC的延长线于点F,BG⊥AF于点G,BG=4![]() ,EF=
,EF=![]() AE,则△CEF的周长为__.
AE,则△CEF的周长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com