
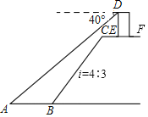
【题目】如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为( )

A. 1.5B. 3
C. 1.5或3D. 有两种情况以上
查看答案和解析>>
科目:初中数学 来源: 题型:
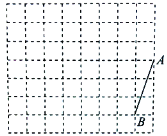
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
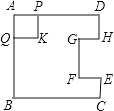
【题目】 如图,在边长为4的正方形纸片ABCD中,从边CD上剪去一个矩形EFGH,且有EF=DH=CE=1cm,FG=2cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止.以AP为边在AP的下方做正方形AQKP,设点P运动时间为t(s),正方形AQKP和纸片重叠部分的面积为S(cm2),则S与t之间的函数关系用图象表示大致是( )
A. 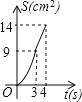 B.
B. 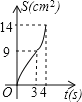
C. 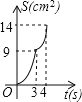 D.
D. 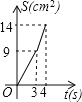
查看答案和解析>>
科目:初中数学 来源: 题型:
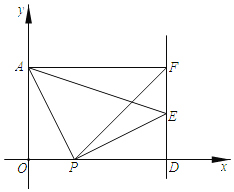
【题目】在平面直角坐标系中,点A坐标为(0,3),x轴上点P(t,0),将线段AP绕点P顺时针旋转90°得到PE,过点E作直线l⊥x轴于D,过点A作AF⊥直线l于F.
(1)当点E是DF的中点时,求直线PE的函数表达式.
(2)当t=5时,求△PEF的面积.
(3)在直线l上是否存在点G,使得∠APO=∠PFD+∠PGD?若存在,试用t的代数式表示点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“淮南牛肉汤”是安徽知名地方小吃.某分店经理发现,当每碗牛肉汤的售价为6元时,每天能卖出500碗;当每碗牛肉汤的售价每增加0.5元时,每天就会少卖出20碗,设每碗牛肉汤的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元/碗的范围是
元/碗的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com