
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

【答案】(1)①证明见解析;②12;③![]() ;(2)当BE为3或2.5或2时,△CDF是等腰三角形.
;(2)当BE为3或2.5或2时,△CDF是等腰三角形.
【解析】
(1)①如图1中,根据AAS证明:△ABE≌△DFA即可.
②利用勾股定理求出BE,即可解决问题.
③如图2中,过点F作FM⊥BC于点M.求出FM,MC即可解决问题.
(2)分三种情形分别求解即可解决问题.
解:(1)①如图1中,
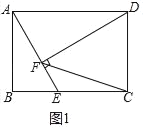
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠B=90°,∴∠AEB=∠DAF.
∵DF⊥AE,∴∠AFD=90°.
∴∠B=∠AFD=90°,
又∵AE=BC,
∴AE=AD,
∴△ABE≌△DFA(AAS).
②如图1中,在Rt△ABE中,∠B=90°,
根据勾股定理,得 BE=![]() =3,
=3,
∵△ABE≌△DFA,
∴DF=AB=DC=4,AF=BE=3.
∵AE=BC=5,∴EF=EC=2,
∴四边形CDFE的周长=2(DC+EC)=2×(4+2)=12.
③如图2中,过点F作FM⊥BC于点M.
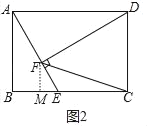
![]() ,
,
在Rt△FME中, ![]() ,
,
![]() ,
,
在Rt△FMC中, ![]() .
.
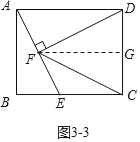
(2)如图3﹣1中,当DF=DC时,则DF=DC=AB=4.
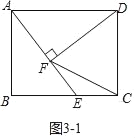
∵∠AEB=∠DAF,∠B=∠AFD=90°,
∴△ABE≌△DFA(AAS).
∴AE=AD=5,
由②可知,BE=3,∴当BE=3时,△CDF是等腰三角形.…
如图3﹣2中,当CF=CD时,过点C作CG⊥DF,垂足为点H,交AD于点G,
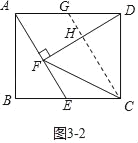
则CG∥AE,DH=FH.
∴AG=GD=2.5.
∵CG∥AE,AG∥EC,
∴四边形AECG是平行四边形,
∴EC=AG=2.5,∴当BE=2.5时,△CDF是等腰三角形.…
如图3﹣中,当FC=FD时,过点F作FQ⊥DC,垂足为点Q.
则AD∥FQ∥BC,DQ=CQ,
∴AF=FE=![]() AE.
AE.
∵∠B=∠AFD=90°,∠AEB=∠DAF,
∴△ABE∽△DFA,
∴![]() ,即AD×BE=AF×AE.
,即AD×BE=AF×AE.
设BE=x,
∴5x=![]() ,
,
解得x1=2,x2=8(不符合题意,舍去)
∴当BE=2时,△CDF是等腰三角形.
综上所述,当BE为3或2.5或2时,△CDF是等腰三角形.


科目:初中数学 来源: 题型:
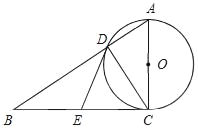
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为参加运动会,某市射击队组织甲、乙、丙三名运动员进行射击测试,每人射击10次,其测试成绩如表:
甲的测试成绩表
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(环) | 8 | 6 | 8 | 7 | 8 | 8 | 9 | 9 | 9 | 8 |
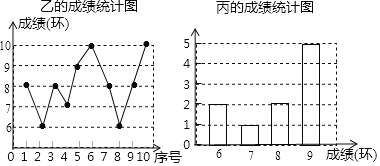
请根据以上图表解决下列问题:
(1)乙运动员测试成绩的众数是 环;丙运动员测试成绩的中位数是 环;
(2)若从三人中选拔一名成绩最稳定的运动员参加本次运动会,你认为选谁更合适?请通过计算明.(参考数据:已知S乙2=1.8,S丙2=1.4)
(3)若准备从甲、乙、丙三人中任意选取两人组合参加团体比赛,由于三人的平均成绩相同,因此三人都符合条件,为了保证公平竞争,现采取抽签的方式产生,请用画树状图或列表格的方法求出选中甲、乙组合的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
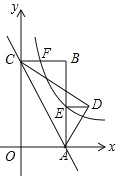
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B的坐标为(![]() ,5),△ACD与△ACO关于直线AC对称(点D和O对应),反比例函数y=
,5),△ACD与△ACO关于直线AC对称(点D和O对应),反比例函数y=![]() (k≠0)的图象与AB,BC分别交于E,F两点,连结DE,若DE∥x轴,则点F的坐标为_____.
(k≠0)的图象与AB,BC分别交于E,F两点,连结DE,若DE∥x轴,则点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
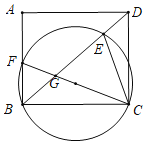
【题目】如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中.
①若BF=2![]() 时,求CE的长.
时,求CE的长.
②当△CEG为等腰三角形时,求所有满足条件的BE的长.
(3)过点E作△BCF外接圆的切线交AD于点P.若PE∥CF且CF=6PE,记△DEP的面积为S1,△CDE的面积为S2,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列几组勾股数:3,4,5; 5,12,13; 7,24,25; 9,40,41…按此规律,当直角三角形的最小直角边长是11时,则较长直角边长是________;当直角三角形的最小直角边长是![]() 时,则较长直角边长是________.
时,则较长直角边长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(m,2),B(﹣3,n)两点关于原点O对称,反比例函数y=![]() 的图象经过点A.
的图象经过点A.
(1)求反比例函数的解析式并判断点B是否在这个反比例函数的图象上;
(2)点P(x1,y1)也在这个反比例函数的图象上,﹣3<x1<m且x1≠0,请直接写出y1的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
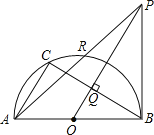
【题目】如图,AB是半圆O的直径,C是半圆O上一点,OQ⊥BC于点Q,过点B作半圆O的切线,交OQ的延长线于点P,PA交半圆O于R,则下列等式中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com