
【题目】为参加运动会,某市射击队组织甲、乙、丙三名运动员进行射击测试,每人射击10次,其测试成绩如表:
甲的测试成绩表
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(环) | 8 | 6 | 8 | 7 | 8 | 8 | 9 | 9 | 9 | 8 |
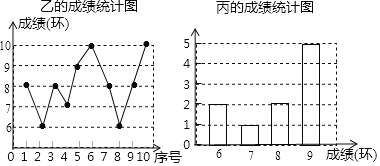
请根据以上图表解决下列问题:
(1)乙运动员测试成绩的众数是 环;丙运动员测试成绩的中位数是 环;
(2)若从三人中选拔一名成绩最稳定的运动员参加本次运动会,你认为选谁更合适?请通过计算明.(参考数据:已知S乙2=1.8,S丙2=1.4)
(3)若准备从甲、乙、丙三人中任意选取两人组合参加团体比赛,由于三人的平均成绩相同,因此三人都符合条件,为了保证公平竞争,现采取抽签的方式产生,请用画树状图或列表格的方法求出选中甲、乙组合的概率是多少?
【答案】(1)8,8.5;(2)成绩最稳定的运动员是甲,应选甲参加本次运动会;(3)![]() .
.
【解析】
(1)根据众数和中位数的定义直接求解即可;
(2)先求出甲的方差,再与乙和丙进行比较,即可得出答案;
(3)根据题意先画出树状图得出所有等情况数和甲、乙组合的情况数,然后根据概率公式求解即可.
(1)∵8环出现了4次,出现的次数最多,
∴乙运动员测试成绩的众数是8环;
把丙运动员测试成绩按从小到大排列,则中位数是![]() =8.5(环),
=8.5(环),
故答案为:8,8.5;
(2)甲的平均数是:![]() (8+6+8+7+8+8+9+9+9+8)=8(环),
(8+6+8+7+8+8+9+9+9+8)=8(环),
则方差是:![]() [5(8﹣8)2+(6﹣8)2+(7﹣8)2+3(9﹣8)2]=0.8,
[5(8﹣8)2+(6﹣8)2+(7﹣8)2+3(9﹣8)2]=0.8,
∵S乙2=1.8,S丙2=1.4,
∴成绩最稳定的运动员是甲,应选甲参加本次运动会;
(3)画树状图如下:

共有6种等情况数,其中甲、乙组合的有2种,
则选中甲、乙组合的概率是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
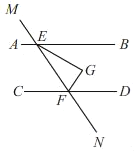
A. 20°B. 25°C. 35°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在四边形纸片ABCD中,AB=12,CD=2,AD=BC=6,∠A=∠B.现将纸片沿EF折叠,使点A的对应点A'落在AB边上,连接A'C.若△A'BC恰好是以A'C为腰的等腰三角形,则AE的长为_____.
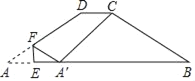
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C.直线y=2经过抛物线上两点D,E.已知点D,E的横坐标分别为x1,x2且满足x1+x2=3,直线BC的表达式为y=﹣x+n.
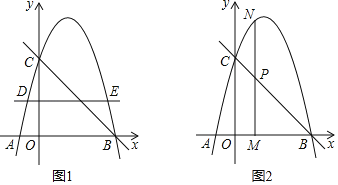
(1)求n的值及抛物线的表达式;
(2)设点Q是直线DE上一动点,问:点Q在什么位置上时,△QOB的周长最小?求出点Q的坐标及△QOB周长的最小值;
(3)如图2,M是线段OB上的一个动点,过点M作垂直于x轴的直线与直线BC和抛物线分别交于点P,N.若点F是直线BC上一个动点,当点P恰好是线段MN的中点时,在坐标平面内是否存在点G,使以点G,F,P,M为顶点的四边形是菱形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,AD=2BC,点E为AD的中点,连接BE、BD,∠ABD=90°.

(1)如图l,求证:四边形BCDE为菱形;
(2)如图2,连接AC交BD于点F,连接EF,若AC平分∠BAD,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABC面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
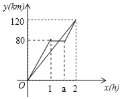
【题目】甲、乙两车分别从A、B两地同时出发,相向而行.甲车中途因故停车一段时间,之后以原速维续行驶到达目的地B,此时乙车同时到达目的地A,如图,是甲、乙两车离各自出发地的路程y(km)与时间x(h)的函数图象.
(1)甲车的速度是 km/h,a的值为 ;
(2)求甲车在整个过程中,y与x的函数关系式;
(3)直接写出甲、乙两车在途中相遇时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com