
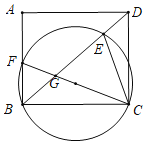
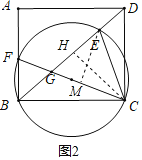
【题目】如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中.
①若BF=2![]() 时,求CE的长.
时,求CE的长.
②当△CEG为等腰三角形时,求所有满足条件的BE的长.
(3)过点E作△BCF外接圆的切线交AD于点P.若PE∥CF且CF=6PE,记△DEP的面积为S1,△CDE的面积为S2,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)①![]() ;②当BE为10,
;②当BE为10,![]() 或
或![]() 时,△CEG为等腰三角形;(3)
时,△CEG为等腰三角形;(3)![]() .
.
【解析】
(1)根据平行线的性质得出∠ABD=∠BDC,根据圆周角定理得出∠ABD=∠ECG,即可证得结论;
(2)根据勾股定理求得BD=10,
①连接EF,根据圆周角定理得出∠CEF=∠BCD=90°,∠EFC=∠CBD.即可得出sin∠EFC=sin∠CBD,得出![]() ,根据勾股定理得到CF=
,根据勾股定理得到CF=![]() ,即可求得CE=
,即可求得CE=![]() ;
;
②分三种情况讨论求得:
当EG=CG时,根据等腰三角形的性质和圆周角定理即可得到∠GEC=∠GCE=∠ABD=∠BDC,从而证得E、D重合,即可得到BE=BD=10;
当GE=CE时,过点C作CH⊥BD于点H,即可得到∠EGC=∠ECG=∠ABD=∠GDC,得到CG=CD=6.根据三角形面积公式求得CH=![]() ,即可根据勾股定理求得GH,进而求得HE,即可求得BE=BH+HE=
,即可根据勾股定理求得GH,进而求得HE,即可求得BE=BH+HE=![]() ;
;
当CG=CE时,过点E作EM⊥CG于点M,由tan∠ECM=![]() .设EM=4k,则CM=3k,CG=CE=5k.得出GM=2k,tan∠GEM=
.设EM=4k,则CM=3k,CG=CE=5k.得出GM=2k,tan∠GEM=![]() ,即可得到tan∠GCH=
,即可得到tan∠GCH=![]() =
=![]() .求得HE=GH=
.求得HE=GH=![]() ,即可得到BE=BH+HE=
,即可得到BE=BH+HE=![]() ;
;
(3)连接OE、EF、AE、EF,先根据切线的性质和垂直平分线的性质得出EF=CE,进而证得四边形ABCD是正方形,进一步证得△ADE≌△CDE,通过证得△EHP∽△FBC,得出EH=![]() BF,即可求得BF=6,根据勾股定理求得CF=10,得出PE=
BF,即可求得BF=6,根据勾股定理求得CF=10,得出PE=![]() ,根据勾股定理求得PH,进而求得PD,然后根据三角形面积公式即可求得结果.
,根据勾股定理求得PH,进而求得PD,然后根据三角形面积公式即可求得结果.
(1)证明:∵AB∥CD.
∴∠ABD=∠BDC,
∵∠ABD=∠ECG,
∴∠ECG=∠BDC.
(2)解:①∵AB=CD=6,AD=BC=8,
∴BD=![]() =10,
=10,
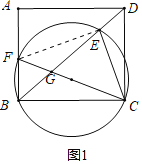
如图1,连结EF,则∠CEF=∠BCD=90°,
∵∠EFC=∠CBD.
∴sin∠EFC=sin∠CBD,
∴![]()
∴CF=![]() =
=![]() ,
,
∴CE=![]() .
.
②Ⅰ、当EG=CG时,∠GEC=∠GCE=∠ABD=∠BDC.
∴E与D重合,
∴BE=BD=10.
Ⅱ、如图2,当GE=CE时,过点C作CH⊥BD于点H,
∴∠EGC=∠ECG=∠ABD=∠GDC,
∴CG=CD=6.
∵CH=![]() ,
,
∴GH=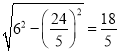 ,
,
在Rt△CEH中,设HE=x,则x2+(![]() )2=(x+
)2=(x+![]() )2
)2
解得x=![]() ,
,
∴BE=BH+HE=![]() +
+![]() =
=![]() ;
;
Ⅲ、如图2,当CG=CE时,
过点E作EM⊥CG于点M.
∵tan∠ECM=![]() .
.
设EM=4k,则CM=3k,CG=CE=5k.
∴GM=2k,tan∠GEM=![]() ,
,
∴tan∠GCH=![]() =tan∠GEM=
=tan∠GEM=![]() .
.
∴HE=GH=![]() ,
,
∴BE=BH+HE=![]() ,
,
综上所述,当BE为10,![]() 或
或![]() 时,△CEG为等腰三角形;
时,△CEG为等腰三角形;
(3)解:∵∠ABC=90°,
∴FC是△BCF的外接圆的直径,设圆心为O,
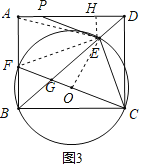
如图3,连接OE、EF、AE、EF,
∵PE是切线,
∴OE⊥PE,
∵PE∥CF,
∴OE⊥CF,
∵OC=OF,
∴CE=EF,
∴△CEF是等腰直角三角形,
∴∠ECF=45°,EF=![]() FC,
FC,
∴∠ABD=∠ECF=45°,
∴∠ADB=∠BDC=45°,
∴AB=AD=8,
∴四边形ABCD是正方形,
∵PE∥FC,
∴∠EGF=∠PED,
∴∠BGC=∠PED,
∴∠BCF=∠DPE,
作EH⊥AD于H,则EH=DH,
∵∠EHP=∠FBC=90°,
∴△EHP∽△FBC,
∴![]() ,
,
∴EH=![]() BF,
BF,
∵AD=CD,∠ADE=∠CDE,
∴△ADE≌△CDE,
∴AE=CE,
∴AE=EF,
∴AF=2EH=![]() BF,
BF,
∴![]() BF+BF=8,
BF+BF=8,
∴BF=6,
∴EH=DH=1,CF=![]() =10,
=10,
∴PE=![]() FC=
FC=![]() ,
,
∴PH=![]() ,
,
∴PD=![]() ,
,
∴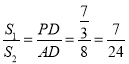 .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,二次函数![]() 与一次函数
与一次函数![]() (a,b为常数,且
(a,b为常数,且![]() ).
).
(1)若y1,y2的图象都经过点(2,3),求y1,y2的表达式;
(2)当y2经过点![]() 时,y1也过A,B两点:
时,y1也过A,B两点:
①求m的值;
②![]() 分别在y1,y2的图象上,实数t使得“当
分别在y1,y2的图象上,实数t使得“当![]() 或
或![]() 时,
时,![]() ”,试求t的最小值.
”,试求t的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,AD=2BC,点E为AD的中点,连接BE、BD,∠ABD=90°.

(1)如图l,求证:四边形BCDE为菱形;
(2)如图2,连接AC交BD于点F,连接EF,若AC平分∠BAD,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABC面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
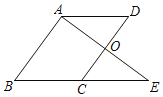
【题目】如图,在四边形ABCD中,AD∥BC,O是CD的中点,延长AO交BC的延长线于点E,且BC=CE.
(1)求证:△AOD≌△EOC;
(2)若∠BAE=90°,AB=6,OE=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.设运动时间为t秒.

(1)求证:△COA∽△AEB;
(2)设△BCD的面积为S当t为何值时,S=![]() ;
;
(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM的内部(不包括边),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
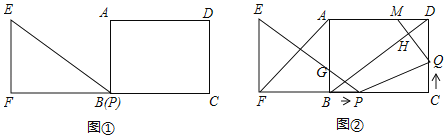
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G,与BD交于点K;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,PQ,当点Q停止运动时,△EFP也停止运动设运动事件为(s)(0<t<6),解答下列问题:
(1)当为何值时,PQ∥BD?
(2)在运动过程中,是否存在某一时刻,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(3)在运动过程中,当t为 秒时,PQ⊥PE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com