
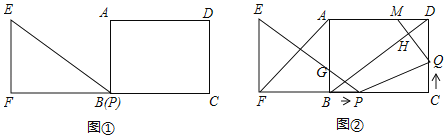
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G,与BD交于点K;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,PQ,当点Q停止运动时,△EFP也停止运动设运动事件为(s)(0<t<6),解答下列问题:
(1)当为何值时,PQ∥BD?
(2)在运动过程中,是否存在某一时刻,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(3)在运动过程中,当t为 秒时,PQ⊥PE.
【答案】(1)![]() (2)t=2s时,S五边形AFPQM:S矩形ABCD=9:8(3)
(2)t=2s时,S五边形AFPQM:S矩形ABCD=9:8(3)![]()
【解析】
(1)利用平行线分线段成比例定理构建方程即可解决问题.
(2)假设存在,由S五边形AFPQM:S矩形ABCD=9:8构建方程即可解决问题.
(3)利用相似三角形的性质构建方程即可解决问题.
解:(1)∵PQ∥BD,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
∴当t=![]() 时,PQ∥BD.
时,PQ∥BD.
(2)假设存在.
∵S五边形AFPQM=S△ABF+S矩形ABCD﹣S△PQC﹣S△MQD
=![]() ×(8﹣t)×6+6×8﹣
×(8﹣t)×6+6×8﹣![]() (8﹣t)×t﹣
(8﹣t)×t﹣![]() ×(6﹣t)×
×(6﹣t)×![]() (6﹣t)
(6﹣t)
=![]() .
.
又∵S五边形AFPQM:S矩形ABCD=9:8,
∴![]() :48=9:8,
:48=9:8,
整理得:t2﹣20t+36=0,
解得t=2或18(舍弃),
∴t=2s时,S五边形AFPQM:S矩形ABCD=9:8.
(3)∵PQ⊥PE,
∴∠QPE=90°,
∵∠EFP=∠C=90°,
∴∠EPF+∠QPC=90°,∠QPC+∠PQC=90°,
∴∠EPF=∠PQC,
∴△EPF∽△PQC,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
∴当t=![]() 时,PQ⊥PE.
时,PQ⊥PE.
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
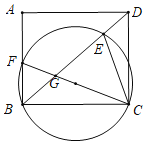
【题目】如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中.
①若BF=2![]() 时,求CE的长.
时,求CE的长.
②当△CEG为等腰三角形时,求所有满足条件的BE的长.
(3)过点E作△BCF外接圆的切线交AD于点P.若PE∥CF且CF=6PE,记△DEP的面积为S1,△CDE的面积为S2,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
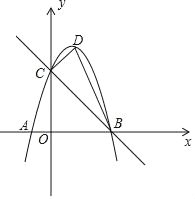
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
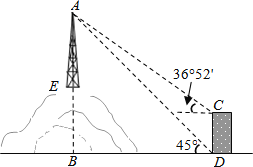
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
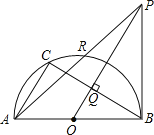
【题目】如图,AB是半圆O的直径,C是半圆O上一点,OQ⊥BC于点Q,过点B作半圆O的切线,交OQ的延长线于点P,PA交半圆O于R,则下列等式中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论:①2a+c<0;②若(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() ,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣
,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣![]() 时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).
时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
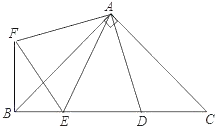
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com