
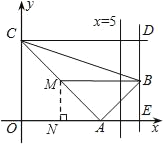
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���C������Ϊ��0��4��������A��ÿ��1����λ�����ٶȣ��ӵ�O������x����������˶���M���߶�AC���е㣮���߶�AM�Ե�AΪ���ģ���˳ʱ�뷽����ת90�㣬�õ��߶�AB������B��x��Ĵ��ߣ�����ΪE������C��y��Ĵ��ߣ���ֱ��BE�ڵ�D�����˶�ʱ��Ϊt�룮

��1����֤����COA�ס�AEB��
��2�����BCD�����ΪS��tΪ��ֵʱ��S��![]() ��
��
��3������MB����MB��OAʱ�����������y��ax2��10ax�Ķ����ڡ�ABM���ڲ����������ߣ�����a��ȡֵ��Χ��
���𰸡���1������������2��t��3��3+5![]() ʱ����3��
ʱ����3��![]() .
.
��������
(1)���ݡ�CAO����ABE����COA����AEB��90�㣬����֤����
(2)���BCD�����ʱ������CDΪ�ס�BDΪ�����⣬��ô��ʾ��BD�ij��ǹؼ���Rt��CAO��Rt��ABE����֪��AC��AB�ı�����ϵ������ͨ�����������εĶ�Ӧ�߳ɱ������BE�ij�����һ���õ�BD�ij����ڱ���BD��ʱ��Ӧ������������ǣ���B���߶�DE�ϣ���B��ED���ӳ����ϣ�
(3)���Ƚ������ߵĽ���ʽ�����䷽���ɵõ������ߵĶ������꣬���������ֱ����ֱ��MB��AB�Ľ���ʽ�У��ɵõ������߶Գ�����������ֱ�ߵĽ������꣬�������������꼴���ж���a��ȡֵ��Χ��
(1)�ߡ�CAO+��BAE��90�㣬��ABE+��BAE��90�㣬
���CAO����ABE��
�ߡ�COA����AEB��90�㣬
���CAO�ס�ABE��
(2)��Rt��CAO��Rt��ABE��֪��BE��![]() ��AE��2��
��AE��2��
��0��t��8ʱ��S��![]() CDBD��
CDBD��![]() (2+t)(4��
(2+t)(4��![]() )��
)��![]() ��
��
��t1��t2��3��
��t��8ʱ��S��![]() CDBD��
CDBD��![]() (2+t)(
(2+t)(![]() ��4)��
��4)��![]() ��
��
��t1��3+5![]() ��t2��3��5
��t2��3��5![]() (Ϊ��������ȥ)��
(Ϊ��������ȥ)��
��t��3��3+5![]() ʱ��S��
ʱ��S��![]() ��
��
(3)��M��MN��x����N����MN��![]() CO��2��
CO��2��
��MB��OAʱ��BE��span>MN��2��OA��2BE��4��
������y��ax2��10ax�Ķ�������Ϊ(5����25a)��
���Ķ�����ֱ��x��5���ƶ���
ֱ��x��5��MB�ڵ�(5��2)����AB�ڵ�(5��1)��
��1����25a��2��
��![]() ��
��


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
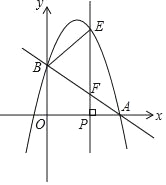
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y��-![]() x+2�ֱ�x�ᡢy���ڵ�A��B��������y����x2+bx+c������A��B����P��x����һ�����㣬����P����ֱ��x���ֱ�߷ֱ������ߺ�ֱ��AB�ڵ�E�͵�F�����P�ĺ�����Ϊm��
x+2�ֱ�x�ᡢy���ڵ�A��B��������y����x2+bx+c������A��B����P��x����һ�����㣬����P����ֱ��x���ֱ�߷ֱ������ߺ�ֱ��AB�ڵ�E�͵�F�����P�ĺ�����Ϊm��
��1����A�������� ����
��2������������������Ӧ�ĺ�������ʽ��
��3����P���߶�OA��ʱ������B��E��FΪ��������������FPA���ƣ���m��ֵ��
��4����E��F��P��������ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩����E��F��P����Ϊ����г�㡱��ֱ��д��E��F��P�����Ϊ����г�㡱ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
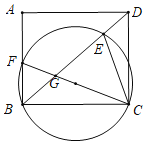
����Ŀ����ͼ������ABCD�У�BC��8����F��AB����һ�㣨�����B�غϣ���BCF�����Բ���Խ���BD�ڵ�E������CF��BD�ڵ�G��
��1����֤����ECG����BDC��
��2����AB��6ʱ���ڵ�F�������˶������У�
����BF��2![]() ʱ����CE�ij���
ʱ����CE�ij���
������CEGΪ����������ʱ������������������BE�ij���
��3������E����BCF���Բ�����߽�AD�ڵ�P����PE��CF��CF��6PE���ǡ�DEP�����ΪS1����CDE�����ΪS2����ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����м��鹴������3��4��5�� 5��12��13�� 7��24��25�� 9,40,41�����˹��ɣ���ֱ�������ε���Сֱ�DZ߳���11ʱ����ϳ�ֱ�DZ߳���________����ֱ�������ε���Сֱ�DZ߳���![]() ʱ����ϳ�ֱ�DZ߳���________��
ʱ����ϳ�ֱ�DZ߳���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Щ��ȫ������Ƶ������������������Ⱥ�ڵ����彡��������Σ����ij�̳������̻�����������ס������ֿ����������������ۣ���ÿ̨���ֿ����������Ľ��۱�ÿ̨���ֿ����������Ľ�����300Ԫ������6000Ԫ�������ֿ�������������������7500Ԫ�������ֿ�����������������ͬ��
��1����ÿ̨���ֿ�����������ÿ̨���ֿ����������Ľ��۷ֱ�Ϊ����Ԫ��
��2�������̳��������ס������ֿ�����������30̨���ҽ������Ѳ�����42000Ԫ�������ٽ������ֿ�������������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(m��2)��B(��3��n)�������ԭ��O�Գƣ�����������y��![]() ��ͼ����A��
��ͼ����A��
(1)���������Ľ���ʽ���жϵ�B�Ƿ������������������ͼ���ϣ�
(2)��P(x1��y1)Ҳ�����������������ͼ���ϣ���3��x1��m��x1��0����ֱ��д��y1�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=xm������P����һ������ǽCD��AD�ľ���ֱ���15m��6m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ���������S�����ֵΪ_____m2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
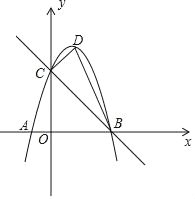
����Ŀ����ͼ����DΪ�����������y=��x2+bx+c��x����A��B���㣬��y���ڵ�C��ֱ��BC�ı���ʽΪy=��x+3��
��1���������ߵı���ʽ��
��2����ֱ��BC����һ��P��ʹPO+PA��ֵ��С�����P�����ꣻ
��3����x�����Ƿ����һ��Q��ʹ����A��C��QΪ��������������BCD���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��b��c�dz�����a��0����x�ύ��A��B���㣬����P��m��n�����������н��ۣ���2a+c��0����������![]() ��y1��������
��y1��������![]() ��y2������
��y2������![]() ��y3�����������ϣ���y1��y2��y3���۹���x�ķ���ax2+bx+k=0��ʵ���⣬��k��c��n���ܵ�n=��
��y3�����������ϣ���y1��y2��y3���۹���x�ķ���ax2+bx+k=0��ʵ���⣬��k��c��n���ܵ�n=��![]() ʱ����ABPΪ����ֱ�������Σ�������ȷ������______����д��ţ���
ʱ����ABPΪ����ֱ�������Σ�������ȷ������______����д��ţ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com