
如图,AB是⊙O的直径,C、P是 上两点,AB=13,AC=5,
上两点,AB=13,AC=5,
(1)如图(1),若点P是 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是 的中点,求PA得长 .
的中点,求PA得长 .

(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得.
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
试题解析::(1)如答图(1),连接PB,
∵AB是⊙O的直径且P是 的中点,∴∠PAB=∠PBA=45°,∠APB=90°.
的中点,∴∠PAB=∠PBA=45°,∠APB=90°.
又∵在等腰三角形△ABC中有AB=13,
∴ .
.

(2)如答图(2),连接BC,与OP相交于M点,作PH⊥AB于点H,
∵P点为 C的中点,∴OP⊥BC,∠OMB=90°,
C的中点,∴OP⊥BC,∠OMB=90°,
又∵AB为直径,∴∠ACB=90°.∴∠ACB=∠OMB. ∴OP∥AC.∴∠CAB=∠POB.
又∵∠ACB=∠OHP=90°,∴△ACB∽△0HP.∴ .
.
又∵ ,∴
,∴ ,解得
,解得 .
.
∴AH=OA+OH=9.
∵在Rt△OPH中,有 。
。
∴在RT△AHP中 有 .
.
∴PA=  .
.

考点:1. 圆心角、弧、弦的关系;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:解答题
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:选择题
如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=( )
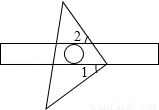
A.40° B.45° C.50° D.60°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:选择题
下列运算正确的是( )
A.x2•x3=x6 B.(x3)3=x9 C.x2+x2=x4 D.x6÷x3=x2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:选择题
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )

A. B.
B. C.
C. D.
D.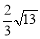
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:解答题
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com