
��֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��P��1��1��ΪԲ�ĵ���P��x�ᣬy��ֱ������ڵ�M�͵�N����F�ӵ�M��������x����������ÿ��1����λ���ȵ��ٶ��˶�������PF������PE��PF��y���ڵ�E�����F�˶���ʱ����t�루t��0��
��1������E��y��ĸ������ϣ���ͼ��ʾ������֤��PE=PF��
��2���ڵ�F�˶������У���OE=a��OF=b�����ú�a�Ĵ���ʽ��ʾb��
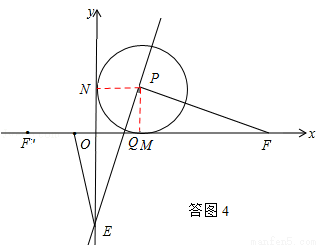
��3������F���ڵ�M�ĶԳƵ�F�䣬����M��E��F������������ߵĶԳ��ύx���ڵ�Q������QE���ڵ�F�˶������У��Ƿ����ijһʱ�̣�ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�

��1��֤������������2��b=2+a��2��a����3����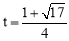 ��
��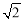 ��
��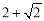 ��
��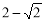 ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
��������
�����������1������PM��PN��������PMF�ա�PNE֤��.
��2���������������t��1ʱ����E��y��ĸ������ϣ�0��t��1ʱ����E��y����������ԭ���ϣ��ٸ��ݣ�1�����.
��3���������������1��t��2ʱ����t��2ʱ������������ʱ������������������ݱ���ʽ���ʱ��t��
���ͼ3����������1��t��2ʱ��
��F��1+t��0����F��F����ڵ�M�Գƣ���F�䣨1��t��0��.
������M��E��F������������ߵĶԳ��ύx���ڵ�Q����Q��1��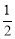 t��0��.��OQ=1��
t��0��.��OQ=1��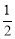 t.
t.
�ɣ�1������PMF�ա�PNE ����NE=MF=t����OE=t��1.
����OEQ�ס�MPFʱ��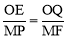 ����
����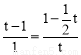 ��
��
��ã�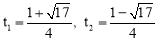 ����ȥ��.
����ȥ��.
����OEQ�ס�MFPʱ��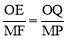 ����
����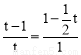 ����ã�
����ã�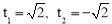 ����ȥ��.
����ȥ��.
���������ͼ4����t��2ʱ��
��F��1+t��0����F��F����ڵ�M�Գƣ���F�䣨1��t��0��
������M��E��F������������ߵĶԳ��ύx���ڵ�Q����Q��1��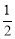 t��0����OQ=
t��0����OQ=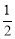 t��1��
t��1��
�ɣ�1������PMF�ա�PNE ��NE=MF=t.��OE=t��1.
����OEQ�ס�MPFʱ��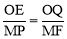 ����
����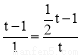 ����.
����.
����OEQ�ס�MFPʱ����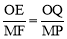 ����
����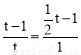 ����ã�
����ã�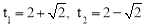 .
.
������������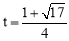 ��
��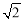 ��
��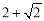 ��
��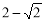 ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
�����������������
��1��֤�������ͼ1������PM��PN��
�ߡ�P��x�ᣬy��ֱ������ڵ�M�͵�N��
��PM��MF��PN��ON��PM=PN
���PMF=��PNE=90������NPM=90��.
��PE��PF����NPE=��MPF=90�㩁��MPE.
����PMF����PNE�� ��
��
���PMF�ա�PNE��ASA��.��PE=PF.
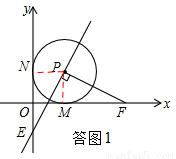
��2������t��1ʱ����E��y��ĸ������ϣ����ͼ1��
�ɣ�1������PMF�ա�PNE����NE=MF=t��PM=PN=1.
��b=OF=OM+MF=1+t��a=NE��ON=t��1��
��b��a=1+t����t��1��=2����b=2+a.
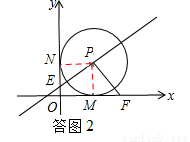
��0��t��1ʱ�����ͼ2����E��y����������ԭ���ϣ�
ͬ����֤��PMF�ա�PNE��
��b=OF=OM+MF=1+t��a=ON��NE=1��t��
��b+a=1+t+1��t=2��
��b=2��a��
��3����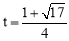 ��
��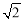 ��
��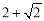 ��
��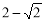 ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
ʱ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ�
���㣺1.���������Գ����⣻2.���ߵ����ʣ�3.ȫ�������ε��ж������ʣ�4.���������ε��ж������ʣ�5.����˼��ͷ���˼���Ӧ��.


 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������人������ѧ�������棩 ���ͣ������
��ͼ��AB����O��ֱ����C��P�� �����㣬AB��13��AC��5��
�����㣬AB��13��AC��5��
��1����ͼ��1��������P�� ���е㣬��PA�ij���
���е㣬��PA�ij���
��2����ͼ��2��������P�� ���е㣬��PA�ó� .
���е㣬��PA�ó� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������˲�������ѧ�������棩 ���ͣ�ѡ����
��ͼ�ļ���������һ��Բ�����һ����������ɵģ������������ĸ���ͼ���� ��

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭��ɽ������ѧ�������棩 ���ͣ������
��ͼ���ڵ����ϵĵ�A���������B������Ϊ���ȣ�AC��7�ף�������BCΪ ��(�ú����Ĵ���ʽ��ʾ)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭��ɽ������ѧ�������棩 ���ͣ�ѡ����
��ͼ����O��ֱ��CD��ֱ��AB�ڵ�E����CE=2��DE=8����AB�ij�Ϊ�� ��

(A)2 (B)4 (C)6 (D)8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
��֪���Ե�OΪԲ�ĵ�����ͬ��Բ�У���Բ����AB��СԲ�ڵ�C��D����ͼ����
��1����֤��AC=BD��
��2������Բ�İ뾶R=10��СԲ�İ뾶r=8����ԲO��ֱ��AB�ľ���Ϊ6����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
��ͼ�����ĸ�С��������ɵļ������У���ÿ��С��������ⳤ����1����ü����帩��ͼ������� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
һ�������Ĵ���װ��20��ֻ����ɫ��ͬ��������5������8������7������
��1����Ӵ�������һ�����ǻ���ĸ��ʣ�
��2���ִӴ���ȡ�����ɸ������Ⱥ�ʹ�Ӵ�������һ������ĸ����� ����Ӵ���ȡ������ĸ���.
����Ӵ���ȡ������ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com