
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.
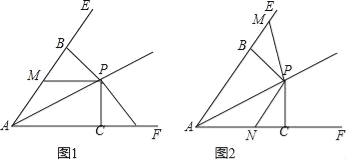
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系 ;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
【答案】(1)、证明过程见解析;(2)、AM+AN=2AC;(3)、32
【解析】
试题分析:(1)、根据PB=PC,∠PBM=∠PCN=90°,利用HL判定Rt△PBM≌Rt△PCN,即可得出BM=CN;
(2)、先已知条件得出AP平分∠CPB,再根据PB⊥AB,PC⊥AC,得到AB=AC,最后根据BM=CN,得出AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;(3)、由AC:PC=2:1,PC=4,即可求得AC的长,又由S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB,即可求得四边形ANPM的面积.
试题解析:(1)、如图1,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°, ∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
![]() , ∴Rt△PBM≌Rt△PCN(HL), ∴BM=CN;
, ∴Rt△PBM≌Rt△PCN(HL), ∴BM=CN;
(2)、AM+AN=2AC. ∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,点P为∠EAF平分线上一点,
∴∠APC=∠APB,即AP平分∠CPB, ∵PB⊥AB,PC⊥AC, ∴AB=AC, 又∵BM=CN,
∴AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;
(3)、如图2,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF, ∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°, ![]() , ∴Rt△PBM≌Rt△PCN(HL),
, ∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN, ∴S△PBM=S△PCN ∵AC:PC=2:1,PC=4, ∴AC=8,
∴由(2)可得,AB=AC=8,PB=PC=4, ∴S四边形ANPM=S△APN+S△APB+S△PBM =S△APN+S△APB+S△PCN
=S△APC+S△APB =![]() ACPC+
ACPC+![]() ABPB=
ABPB=![]() ×8×4+
×8×4+![]() ×8×4=32.
×8×4=32.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
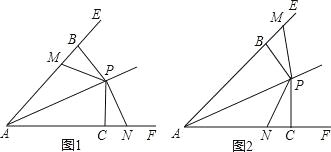
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接BF,
求证:AE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题: 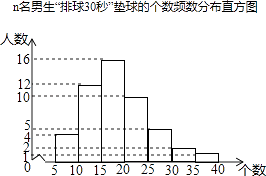
(1)求n的值.
(2)这个样本数据的中位数落在第组.
(3)若测试九年级男生“排球30秒”对墙垫球个数不低于10个为合格,根据统计结果,估计该校九年级450名男同学成绩合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M. 
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣9. 
(1)求证:无论m为何值,该抛物线与x轴总有两个交点;
(2)该抛物线与x轴交于A,B两点,点A在点B的左侧,且OA<OB,与y轴的交点坐标为(0,﹣5),求此抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与x轴的交点为N,若点M是线段AN上的任意一点,过点M作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D,点P是线段MC上一点,且满足MP= ![]() MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.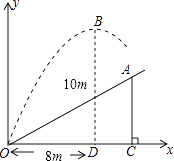
(1)求点A的坐标;
(2)求球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营儿童玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是200件,而销售单价每上涨2元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时,月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2280元?
(3)每件玩具的售价定为多少元时,月销售利润达到最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题
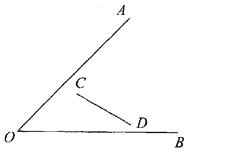
(1)如图:已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(尺规作图,不写作法,保留作图痕迹,写出结论);
(2)如图:在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
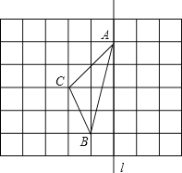
①在图中画出与关于直线![]() 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;
②线段CC′被直线![]() _________;
_________;
③△ABC的面积为_________;
④在直线![]() 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com