
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣9. 
(1)求证:无论m为何值,该抛物线与x轴总有两个交点;
(2)该抛物线与x轴交于A,B两点,点A在点B的左侧,且OA<OB,与y轴的交点坐标为(0,﹣5),求此抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与x轴的交点为N,若点M是线段AN上的任意一点,过点M作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D,点P是线段MC上一点,且满足MP= ![]() MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】
(1)证明:令y=0,则x2﹣2mx+m2﹣9=0,
∵△=(﹣2m)2﹣4m2+36>0,
∴无论m为何值时方程x2﹣2mx+m2﹣9=0总有两个不相等的实数根,
∵抛物线y=x2﹣2mx+m2﹣9的开口向上,顶点在x轴的下方,
∴该抛物线与x轴总有两个交点.
(2)解:∵抛物线y=x2﹣2mx+m2﹣9与y轴交点坐标为(0,﹣5),
∴﹣5=m2﹣9.
解得:m=±2.
当m=﹣2,y=0时,x2+4x﹣5=0
解得:x1=﹣5,x2=1,
∵抛物线y=x2﹣2mx+m2﹣9与x轴交于A,B两点(点A在点B的左侧,且OA<OB),
∴m=﹣2不符合题意,舍去.
∴m=2.
∴抛物线的解析式为y=x2﹣4x﹣5;

(3)解:如图2,假设E点存在,
∵MC⊥EM,CD⊥MC,
∴∠EMP=∠PCD=90°.
∴∠MEP+∠MPE=90°
∵PE⊥PD,
∴∠EPD=90°,
∴∠MPE+∠DPC=90°
∴∠MEP=∠CPD.
在△EMP和△PCD中,
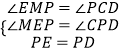 ,
,
∴△EPM≌△PDC(AAS).
∴PM=DC,EM=PC
设C(x0,y0),则D(4﹣x0,y0),P(x0, ![]() y0).
y0).
∴2x0﹣4= ![]() y0.
y0.
∵点C在抛物线y=x2﹣4x﹣5上;
∴y0═x02﹣4x0﹣5
∴2x0﹣4= ![]() (x02﹣4x0﹣5).
(x02﹣4x0﹣5).
解得:x01=1,x02=11(舍去),
∴P(1,﹣2).
∴PC=6.∴ME=PC=6.
∴E(7,0).
【解析】(1)令y=0,则x2﹣2mx+m2﹣9=0,根据根的判别式b2﹣4ac=(﹣2m)2﹣4(m2﹣9)=36>0,所以无论m为何值,该抛物线与x轴总有两个交点.(2)直接将C点(0,﹣5)代入y=x2﹣2mx+m2﹣9根据抛物线与x轴交于A,B两点(点A在点B的左侧,且OA<OB),求出m的值即可;(3)假设E点存在由直角三角形的性质可以得出∠MEP=∠CPD.再根据条件可以得出△EPM≌△PDC就有PM=DC,EM=PC,设C(x0 , y0),则D(4﹣x0 , y0),P(x0 , ![]() y0).根据PM=DC就有2x0﹣4=﹣
y0).根据PM=DC就有2x0﹣4=﹣ ![]() y0 , 由C点在抛物线上有2x0﹣4=﹣
y0 , 由C点在抛物线上有2x0﹣4=﹣ ![]() ( x02﹣4x0﹣5),求出x0的值就可以得出结论.
( x02﹣4x0﹣5),求出x0的值就可以得出结论.


科目:初中数学 来源: 题型:
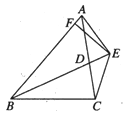
【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.
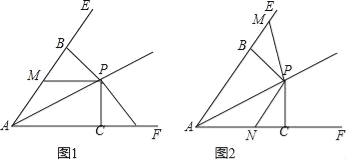
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系 ;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) 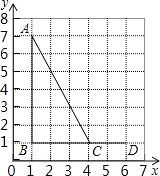
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
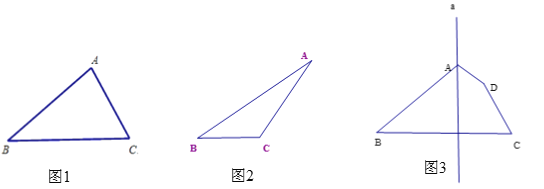
(1)用直尺和圆规作图(不写作法,保留作图痕迹)在图1中,作△ABC的角平分线BD; 在图2中,作△ABC的高AE;
(2)在图3中,画出下列图形关于直线a的对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
A.a确定抛物线的形状与开口方向
B.若将抛物线C沿y轴平移,则a,b的值不变
C.若将抛物线C沿x轴平移,则a的值不变
D.若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com