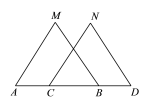
【题目】如图，已知点A、C、B、D在同一条直线上，AC＝BD，AM＝CN，BM＝DN，
求证：（1）△ABM ≌△CDN； （2）AM∥CN．
【答案】(1)见解析;(2)见解析
【解析】
（1）首先根据AC=BD可得AB=CD，再加上条件AM=CN，BM=DN可利用SSS定理证明△AMB≌△CND．
(2) 首先根据AC=BD可得AB=CD，再加上条件AM=CN，BM=DN可利用SSS定理证明△AMB≌△CND，再根据全等三角形的性质可得∠A=∠NCD，即可证明AM∥CN．
解：（1）证明：∵AC=BD，
∴AC+CB=DB+CB，
即：AB=CD，
AC=BD在△AMB和△CND中，
，
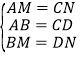∴△AMB≌△CND（SSS）．
(2) 证明：∵AC=BD，
∴AC+CB=DB+CB，
即：AB=CD，
AC=BD在△AMB和△CND中，
，
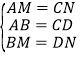∴△AMB≌△CND（SSS），
∴∠A=∠NCD，
∴AM∥CN．
科目：初中数学 来源： 题型：
【题目】如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（﹣2，4）、（﹣2，0）、（﹣4，1），将△ABC绕原点O旋转180度得到△A1B1C1 ． 结合所给的平面直角坐标系解答下列问题：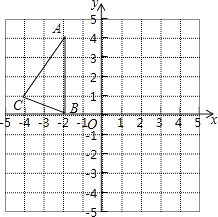 
（1）画出△A1B1C1；
（2）画出一个△A2B2C2 ， 使它分别与△ABC，△A1B1C1轴对轴（其中点A，B，C与点A2 ， B2 ， C2对应）；
（3）在（2）的条件下，若过点B的直线平分四边形ACC2A2的面积，请直接写出该直线的函数解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在所给正方形网格图中完成下列各题：（用直尺画图，保留痕迹）
（1）画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；
（2）在DE上画出点Q，使QA+QC最小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置，使A、C、B′三点共线，那么旋转角度的大小为（ ）
A.45°
B.90°
C.120°
D.135°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A(a,b)，B(c,0)，|a-3|+(2b-c)2+
=0.
(1)求点A，B的坐标；
(2)如图，点C为x轴正半轴上一点，且OC＝OA，点D为OC的中点，连AC，AD，请探索AD＋CD与
AC之间的大小关系，并说明理由；
(3)如图，过点A作AE⊥y轴于E，F为x轴负半轴上一动点（ 不与(－3,0)重合 ），G在EF延长线上，以EG为一边作∠GEN＝45°，过A作AM⊥x轴，交EN于点M，连FM，当点F在x轴负半轴上移动时，式子
的值是否发生变化？若变化，求出变化的范围；若不变化，请求出其值并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M，N分别是射线AE，AF上的点，且PM=PN．
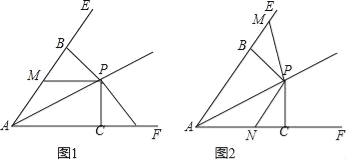
（1）如图1，当点M在线段AB上，点N在线段AC的延长线上时，求证：BM=CN；
（2）在（1）的条件下，直接写出线段AM，AN与AC之间的数量关系 ；
（3）如图2，当点M在线段AB的延长线上，点N在线段AC上时，若AC：PC=2：1，且PC=4，求四边形ANPM的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
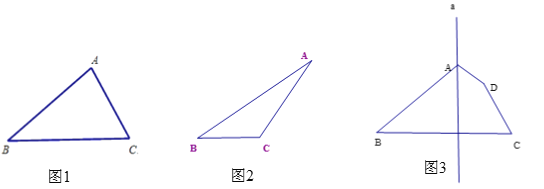
【题目】作图题:
（1）用直尺和圆规作图(不写作法，保留作图痕迹)在图1中，作△ABC的角平分线BD； 在图2中，作△ABC的高AE；
（2）在图3中，画出下列图形关于直线a的对称图形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点A旋转60°到△ADE的位置，点C的对应点为E，连接CD，若AC=BC=1，则CD的长为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
