
| 3 |
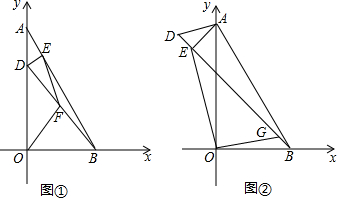
| GB |
| AE |
| 3 |
| GB |
| AE |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
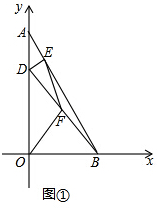 解:(Ⅰ)如图①,
解:(Ⅰ)如图①,| 1 |
| 2 |
| GB |
| AE |
| OB |
| OA |
| 3 |
| 3 |
| GB |
| AE |
| 6 | ||
6
|
| ||
| 3 |
| 3 |
(6
|
| AE |
| AO |
| DE |
| BO |
| AD |
| AB |
| 3 |
| AE | ||
6
|
| DE |
| 6 |
2
| ||
| 12 |
| 3 |
| BG |
| AE |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 122-32 |
| 15 |
| 15 |
| 3 |
3
| ||||
| 2 |
3
| ||||
| 2 |


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
| k |
| x |
| km |
| 4 |
| A、m=-1,n=0 |
| B、m=0,n=-1 |
| C、m=1,n=-1 |
| D、m=-1,n=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
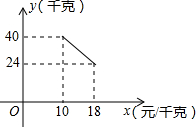 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4),B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4),B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com