
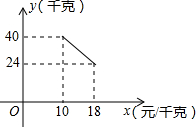
 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
|
|


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
| A、9 800名学生是总体 |
| B、每个学生是个体 |
| C、100名学生是所抽取的一个样本 |
| D、样本容量是100 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=
如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=| k2 |
| x |
| k2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
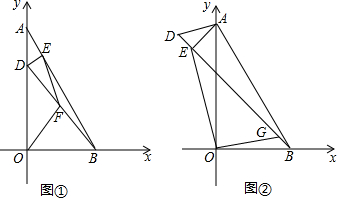
| GB |
| AE |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
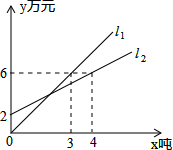 如图,l1反映了某产品的销售收入与销售量之间的关系,l2反映了该产品的销售城北与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.
如图,l1反映了某产品的销售收入与销售量之间的关系,l2反映了该产品的销售城北与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
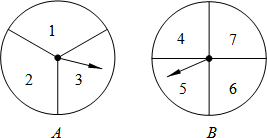 甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com