
【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小;
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.

【答案】(1)∠EAD=20°;(2)2∠EAD=∠C∠B,理由见解析.
【解析】分析:(1)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=![]() ∠BAC,故∠EAD=∠EAC-∠DAC;(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
∠BAC,故∠EAD=∠EAC-∠DAC;(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
本题解析:
(1)∵∠B=30°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是角平分线,∴ ∠EAC=![]() ∠BAC=40°,∵AD是高,∠C=70°,
∠BAC=40°,∵AD是高,∠C=70°,
∴∠DAC=90°﹣∠C=20°,∴∠EAD=∠EAC﹣∠DAC=40°﹣20°=20°;
(2)由(1)知,∠EAD=∠EAC﹣∠DAC=![]() ∠BAC﹣(90°﹣∠C)①,
∠BAC﹣(90°﹣∠C)①,
把∠BAC=180°﹣∠B﹣∠C代入①,整理得∠EAD=![]() ∠C﹣
∠C﹣![]() ∠B,
∠B,
∴2∠EAD=∠C﹣∠B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
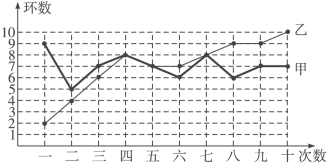
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,一季度的营业额为728万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )
A.20%
B.45%
C.65%
D.91%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF 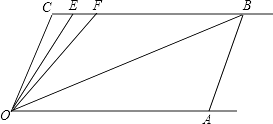
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF,现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当边CD′恰好经过EF的中点H时,求旋转角α的大小;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△BCD′能否全等?若能,直接写出旋转角α的大小;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com