练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AD⊥BC，GC⊥BC，CF⊥AB，垂足分别是D、C、F，下列说法中，错误的是（　　）

    A. △ABC中，AD是边BC上的高

    B. △ABC中，GC是边BC上的高

    C. △GBC中，GC是边BC上的高

    D. △GBC中，CF是边BG上的高

    【答案】B

    【解析】试题分析：A、AD经过△ABC的一个顶点，且AD垂直于BC边所在的直线，所以△ABC中AD是边BC上的高，故此选项正确；

    B、GC没有经过BC所对的顶点A，所以△ABC中，GC不是BC边上的高，故此选项错误；

    C、GC经过△GBC的一个顶点，且GC垂直于BC，所以△GBC中GC是边BC上的高，故此选项正确；

    D、CF经过△GBC的一个顶点，且CF垂直于BG，所以△GBC中CF是边BG上的高，故此选项正确．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AD⊥BC，AE平分∠BAC交BC于点E．

    （1）∠B=30°，∠C=70°，求∠EAD的大小；

    （2）若∠B＜∠C，则2∠EAD与∠C-∠B是否相等？若相等，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：2（x﹣3）2=x2﹣9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，A1，A2，A3，…，An为AC边上不同的n个点，首先连接BA1，图中出现了3个不同的三角形，再连接BA2，图中便有6个不同的三角形…

    （1）完成下表：

    连接个数

    出现三角形个数

    若出现了45个三角形，则共连接了多少个点？

    若一直连接到An，则图中共有__________个三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的长．

    小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图 2）．

    请回答：∠ACE的度数为 ，AC的长为 ．

    参考小腾思考问题的方法，解决问题：

    如图 3，在四边形 ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2ED，求BC的长．

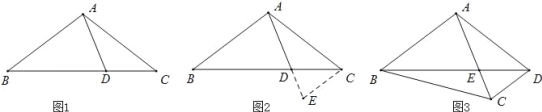
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一条抛物线经过(－2，5)，(0，－3)和(1，－4)三点．

    (1)求此抛物线的表达式；

    (2)假如这条抛物线与x轴交于点A，B，与y轴交于点C，已知点A在点B左侧，试判断△OCB的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形中，对称轴的数量小于3的是

    A. 菱形B. 正方形

    C. 正五边形D. 等边三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣ ）﹣1+（﹣2）2×50﹣（﹣ ）﹣2；
    （2）2a5﹣a2a3+（2a4）2÷a3 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个直角三角形中，两条直角边分别为， ，斜边为：

    （1）如果， ，则 ，三角形的周长为 ，面积为 ；

    （2）如果， ，则三角形的周长为 ，面积为 ；

    （3）如果， ，则 ，

    查看答案和解析>>

    同步练习册答案