
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,过
两点,过![]() 、
、![]() 两点分别作
两点分别作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )
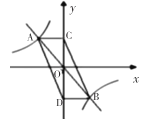
A.4B.8C.12D.24
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
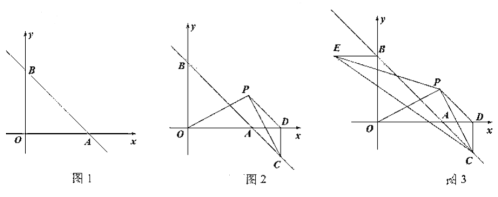
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点![]() 在第一象限内,连接
在第一象限内,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的而积为S,求S与
的而积为S,求S与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a,0),B(0,b),且a,b满足a2-2ab+b2+(b-4)2=0,点C为线段AB上一点,连接OC.
(1)直接写出a=____,b=_____;
(2)如图1,P为OC上一点,连接PA,PB.若PA=B0,∠BPC=30°.求点P的纵坐标;
(3)如图2,在(2)的条件下,点M是AB上一动点,以OM为边在OM的右侧作等边△OMN,连接CN.若OC=t,求ON+CN的最小值(结果用含t的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】收发微信红包已成为各类人群进行交流联系,增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?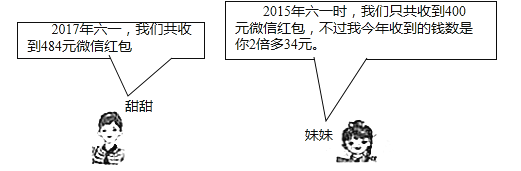
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已如如图1,在平面直角坐标系中,点A的坐标为(6,0)、点B的坐标为(0,8),点C在y轴上,作直线AC.点B关于直线AC的对称点B′刚好在x轴上,连接CB′.
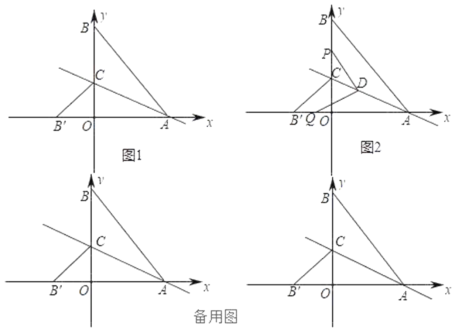
(1)写出点B′的坐标,并求出直线AC对应的函数表达式;
(2)点D在线段AC上,连接DB、DB′、BB′,当△DBB′是等腰直角三角形时,求点D坐标;
(3)如图2,在(2)的条件下,点P从点B出发以每秒2个单位长度的速度向原点O运动,到达点O时停止运动,连接PD,过D作DP的垂线,交x轴于点Q,问点P运动几秒时△ADQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.
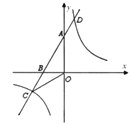
(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励在学校体育艺术节中表现突出的25名同学,派李老师为这些同学购买奖品,要求每人一件.李老师到文具店看了商品后,决定奖品在钢笔和笔记本中选择.如果买4个笔记本和2支钢笔,则需86元;如果买3个笔记本和1支钢笔,则需57元.
(1)求笔记本和钢笔的单价分别为多少元?
(2)售货员提示,购买笔记本没有优惠;买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠,若买x(x>10)支钢笔,所需总费用为y元,请你求出y与x之间的函数关系式;
(3)在(2)的条件下,如果买同一种奖品,请你帮忙计算说明,买哪种奖品费用更低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
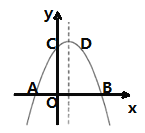
如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点坐标为点
,顶点坐标为点![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 最小时,求点
最小时,求点![]() 坐标;
坐标;
(3)在第一象限的抛物线上有一点![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 坐标;
坐标;
(4)在![]() 轴下方抛物线上有一点
轴下方抛物线上有一点![]() ,
,![]() 面积为6,请直接写出点
面积为6,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
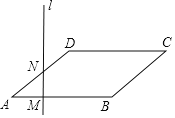
【题目】如图,点![]() 为平行四边形
为平行四边形![]() 的边
的边![]() 上一动点,过点
上一动点,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() ,且直线
,且直线![]() 与平行四边形
与平行四边形![]() 的另一边交于点
的另一边交于点![]() .当点
.当点![]() 从
从![]() 匀速运动时,设点
匀速运动时,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,能大致反映
,能大致反映![]() 与
与![]() 函数关系的图象是( )
函数关系的图象是( )
A.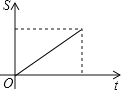 B.
B.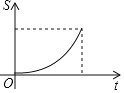
C.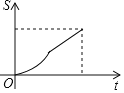 D.
D.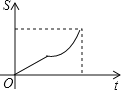
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com