
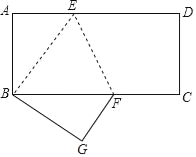
ĄžĖâÄŋĄŋŌŅČįČįÍŧ1ŖŦÔÚÆŊÃæÖąŊĮ×øąęĪĩÖĐŖŦĩãAĩÄ×øąęÎĒ(6ŖŦ0)ĄĸĩãBĩÄ×øąęÎĒ(0ŖŦ8)ŖŦĩãCÔÚyÖáÉĪŖŦ×÷ÖąĪßACŖŽĩãBšØĶÚÖąĪßACĩÄļÔŗÆĩãBĄä¸ÕēÃÔÚxÖáÉĪŖŦÁŦŊĶCBĄäŖŽ
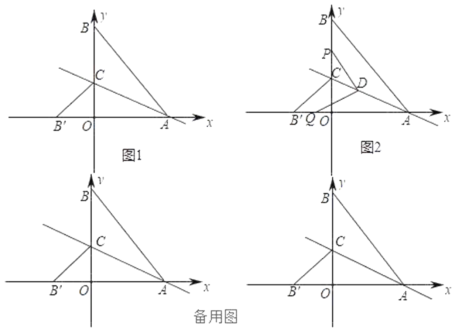
Ŗ¨1ŖŠĐ´ŗöĩãBĄäĩÄ×øąęŖŦ˛ĸĮķŗöÖąĪßACļÔĶĻĩÄē¯Ęũąí´īĘŊŖģ
Ŗ¨2ŖŠĩãDÔÚĪßļÎACÉĪŖŦÁŦŊĶDBĄĸDBĄäĄĸBBĄäŖŦĩąĄ÷DBBĄäĘĮĩČŅüÖąŊĮČũŊĮĐÎĘąŖŦĮķĩãD×øąęŖģ
Ŗ¨3ŖŠČįÍŧ2ŖŦÔÚŖ¨2ŖŠĩÄĖõŧūĪÂŖŦĩãP´ĶĩãBŗöˇĸŌÔÃŋÃë2¸öĩĨÎģŗ¤ļČĩÄËŲļČĪōÔĩãOÔËļ¯ŖŦĩŊ´īĩãOĘąÍŖÖšÔËļ¯ŖŦÁŦŊĶPDŖŦšũD×÷DPĩÄ´šĪßŖŦŊģxÖáĶÚĩãQŖŦÎĘĩãPÔËļ¯ŧ¸ÃëĘąĄ÷ADQĘĮĩČŅüČũŊĮĐÎŖŽ
Ąž´đ°¸ĄŋŖ¨1ŖŠB'(Š4ŖŦ0)ŖŦyŖŊŠ![]() x+3ŖģŖ¨2ŖŠD(2ŖŦ2)ŖģŖ¨3ŖŠĩãPĩÄÔËļ¯ĘąŧäÎĒ1Ãëģō5Š
x+3ŖģŖ¨2ŖŠD(2ŖŦ2)ŖģŖ¨3ŖŠĩãPĩÄÔËļ¯ĘąŧäÎĒ1Ãëģō5Š![]() Ãë
Ãë
ĄžŊâÎöĄŋ
Ŗ¨1ŖŠĶÉĖâŌâĮķŗö![]() ŖŦ¸ųžŨ
ŖŦ¸ųžŨ![]() Ķë
Ķë![]() šØĶÚÖąĪß
šØĶÚÖąĪß![]() ļÔŗÆŖŦĮķŗö
ļÔŗÆŖŦĮķŗö![]() ×øąęŖŦÉčĩã
×øąęŖŦÉčĩã![]() ŖŦĮķŗö
ŖŦĮķŗö![]() ŖŦÉčÖąĪß
ŖŦÉčÖąĪß![]() ĩÄŊâÎöĘŊÎĒ
ĩÄŊâÎöĘŊÎĒ![]() ŖŦ°ŅAŖŦC´úČëŋÉĩÃACąí´īĘŊŖģ
ŖŦ°ŅAŖŦC´úČëŋÉĩÃACąí´īĘŊŖģ
Ŗ¨2ŖŠĶÉŌŅÖĒŋÉĩÃ![]() ĘĮĩČŅüÖąŊĮČũŊĮĐÎŖŦšũĩã
ĘĮĩČŅüÖąŊĮČũŊĮĐÎŖŦšũĩã![]() ×÷
×÷![]() ÖáŖŦ
ÖáŖŦ![]() ÖáŖŦÖ¤Ã÷
ÖáŖŦÖ¤Ã÷ ![]() ŖŦĩÃŗö
ŖŦĩÃŗö![]() ŖŦÉčĩã
ŖŦÉčĩã![]() ´úČë
´úČë![]() ÖĐŖŦŧ´ŋÉĮķŗöĩãD×øąęŖģ
ÖĐŖŦŧ´ŋÉĮķŗöĩãD×øąęŖģ
Ŗ¨3ŖŠĶÉŖ¨2ŖŠŋÉĩÃ![]() ŖŦÖ¤Ã÷
ŖŦÖ¤Ã÷![]() ŖŦĩÃĩŊ
ŖŦĩÃĩŊ![]() ŖŦˇÖĸŲĩą
ŖŦˇÖĸŲĩą![]() ĘąŖŦĸÚĩą
ĘąŖŦĸÚĩą![]() ĘąŖŦĸÛĩą
ĘąŖŦĸÛĩą![]() ĘąŖŦČũÖÖĮéŋöˇÖąđŊøĐĐĖÖÂÛ.
ĘąŖŦČũÖÖĮéŋöˇÖąđŊøĐĐĖÖÂÛ.
ŊâŖēŖ¨1ŖŠĄßAĩÄ×øąęÎĒŖ¨6ŖŦ0ŖŠĄĸĩãBĩÄ×øąęÎĒŖ¨0ŖŦ8ŖŠŖŦ
ĄāOAŖŊ6ŖŦOBŖŊ8ŖŦ
ĄßĄĪAOBŖŊ90ĄãŖŦ
ĄāABŖŊ10ŖŦ
ĄßBĶëBĄäšØĶÚÖąĪßACļÔŗÆŖŦ
ĄāAC´šÖąÆŊˇÖBBĄäŖŦ
ĄāBCŖŊCBĄäŖŦAB'ŖŊABŖŊ10ŖŦ
ĄāBĄäŖ¨Š4ŖŦ0ŖŠŖŦ
ÉčĩãCŖ¨0ŖŦmŖŠŖŦ
ĄāOCŖŊmŖŦ
ĄāCBĄäŖŊCBŖŊ8ŠmŖŦ
ĄßÔÚRtĄ÷COBĄäÖĐŖŦĄĪCOBĄäŖŊ90ĄãŖŦ
Ąām2+16ŖŊŖ¨8ŠmŖŠ2ŖŦ
ĄāmŖŊ3ŖŦ
ĄāCŖ¨0ŖŦ3ŖŠŖŦ
ÉčÖąĪßACĩÄŊâÎöĘŊÎĒyŖŊkx+bŖ¨kĄŲ0ŖŠŖŦ
°ŅAŖ¨6ŖŦ0ŖŠŖŦCŖ¨0ŖŦ3ŖŠ´úČëŋÉĩÃkŖŊ-![]() ŖŦbŖŊ3ŖŦ
ŖŦbŖŊ3ŖŦ
ĄāyŖŊ-![]() x+3Ŗģ
x+3Ŗģ
Ŗ¨2ŖŠĄßAC´šÖąÆŊˇÖBBĄäŖŦ
ĄāDBŖŊDBĄäŖŦ
ĄßĄ÷BDBĄäĘĮĩČŅüÖąŊĮČũŊĮĐÎŖŦ
ĄāĄĪBDBĄäŖŊ90ĄãŖŦ
šũĩãD×÷DEĄÍxÖáŖŦDFĄÍyÖáŖŦ
ĄāĄĪDFOŖŊĄĪDFBŖŊĄĪDEBĄäŖŊ90ĄãŖŦ
ĄßĄĪEDFŖŊ360ĄãŠĄĪDFBŠĄĪDEOŠĄĪEOFŖŦĄĪEOFŖŊ90ĄãŖŦ
ĄāĄĪEDFŖŊ90ĄãŖŦ
ĄāĄĪEDFŖŊĄĪBDBĄäŖŦ
ĄāĄĪBDFŖŊĄĪEDBĄäŖŦ
ĄāĄ÷FDBĄÕĄ÷EDBĄäŖ¨AASŖŠŖŦ
ĄāDFŖŊDEŖŦ
ÉčĩãDŖ¨aŖŦaŖŠ´úČëyŖŊŠ![]() x+3ÖĐŖŦ
x+3ÖĐŖŦ
ĄāaŖŊ2ŖŦ
ĄāDŖ¨2ŖŦ2ŖŠŖģ
Ŗ¨3ŖŠÍŦŖ¨2ŖŠŋÉĩÃĄĪPDFŖŊĄĪQDEŖŦ
ĄßDFŖŊDEŖŊ2ŖŦĄĪPDFŖŊĄĪQDEŖŊ90ĄãŖŦ
ĄāĄ÷PDFĄÕĄ÷QDEŖ¨AASŖŠŖŦ
ĄāPFŖŊQEŖŦ
ĸŲĩąDQŖŊDAĘąŖŦ
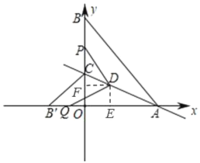
ĄßDEĄÍxÖáŖŦ
ĄāQEŖŊAEŖŊ4ŖŦ
ĄāPFŖŊQEŖŊ4ŖŦ
ĄāBPŖŊBFŠPFŖŊ2ŖŦ
ĄāĩãPÔËļ¯ĘąŧäÎĒ1ÃëŖģ
ĸÚĩąAQŖŊADĘąŖŦ

ĄßAŖ¨6ŖŦ0ŖŠĄĸDŖ¨2ŖŦ2ŖŠŖŦ
ĄāADŖŊ2![]() ŖŦ
ŖŦ
ĄāAQŖŊ2![]() Š4ŖŦ
Š4ŖŦ
ĄāPFŖŊQEŖŊ2![]() Š4ŖŦ
Š4ŖŦ
ĄāBPŖŊBFŠPFŖŊ10Š2![]() ŖŦ
ŖŦ
ĄāĩãPĩÄÔËļ¯ĘąŧäÎĒ5Š![]() ÃëŖģ
ÃëŖģ
ĸÛĩąQDŖŊQAĘąŖŦ
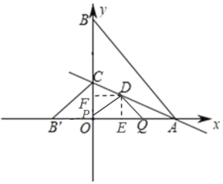
ÉčQEŖŊnŖŦ
ÔōQDŖŊQAŖŊ4ŠnŖŦ
ÔÚRtĄ÷DEQÖĐŖŦĄĪDEQŖŊ90ĄãŖŦ
Ąā4+n2ŖŊŖ¨4ŠnŖŠ2ŖŦ
ĄānŖŊ1.5ŖŦ
ĄāPFŖŊQEŖŊ1.5ŖŦ
ĄāBPŖŊBF+PFŖŊ7.5ŖŦ
ĄāĩãPĩÄÔËļ¯ĘąŧäÎĒ7.5ÃëŖŦ
Ąß0ĄÜtĄÜ4ŖŦ
ĄātŖŊ7.5ÉáČĨŖŦ
×ÛÉĪËųĘöŖēĩãPĩÄÔËļ¯ĘąŧäÎĒ1Ãëģō5Š![]() ÃëŖŽ
ÃëŖŽ


 ÔÄļÁŋėŗĩĪĩÁĐ´đ°¸
ÔÄļÁŋėŗĩĪĩÁĐ´đ°¸
| Äęŧļ | ¸ßÖĐŋÎŗĖ | Äęŧļ | ŗõÖĐŋÎŗĖ |
| ¸ßŌģ | ¸ßŌģÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõŌģ | ŗõŌģÃâˇŅŋÎŗĖÍÆŧöŖĄ |
| ¸ßļū | ¸ßļūÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõļū | ŗõļūÃâˇŅŋÎŗĖÍÆŧöŖĄ |
| ¸ßČũ | ¸ßČũÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõČũ | ŗõČũÃâˇŅŋÎŗĖÍÆŧöŖĄ |
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
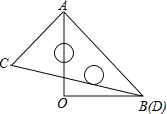
ĄžĖâÄŋĄŋČįÍŧŖŦŊĢŌģąßŗ¤ABÎĒ4ĩÄžØĐÎÖŊÆŦÕÛĩūŖŦĘšĩãDĶëĩãBÖØēĪŖŦÕÛēÛÎĒEFŖŦČôEFŖŊ2![]() ŖŦÔōžØĐÎĩÄÃæģũÎĒŖ¨ĄĄĄĄŖŠ
ŖŦÔōžØĐÎĩÄÃæģũÎĒŖ¨ĄĄĄĄŖŠ
A.32B.28C.30D.36
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
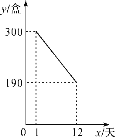
ĄžĖâÄŋĄŋÄŗšĢËžŋĒˇĸŗöŌģŋîĐ°ü×°ĩÄÅŖÄĖŖŦÅŖÄĖĩÄŗÉąžŧÛÎĒ6ÔĒ/ēĐŖŦÕâÖÖĐ°ü×°ĩÄÅŖÄĖÔÚÕũĘŊÍļˇÅĘĐŗĄĮ°Í¨šũ´úĪúĩãŊøĐĐÁËÎĒÆÚŌģ¸öÔÂ(30Ėė)ĩÄĘÔĶĒĪúŖŦĘÛŧÛÎĒ8ÔĒ/ēĐŖŽĮ°ŧ¸ĖėĩÄĪúÁŋÃŋŋöĶúĪÂŖŦš¤×÷ČËÔąļÔĪúĘÛĮéŋöŊøĐĐÁ˸ú×ŲŧĮÂŧŖŦ˛ĸŊĢŧĮÂŧĮéŋöģæŗÉÍŧĪķŖŦÍŧÖĐĩÄĪßļÎąíĘžĮ°12ĖėČÕĪúĘÛÁŋy(ēĐ)ĶëĪúĘÛĘąŧäx(Ėė)ÖŽŧäĩÄē¯ĘũšØĪĩŖŦĶÚĘĮ´ĶĩÚ13ĖėÆđ˛ÉĶôōÕÛĪúĘÛ(˛ģĩÍĶÚŗÉąžŧÛ)ŖŦĘąŧäÃŋÔöŧĶ1ĖėŖŦČÕĪúĘÛÁŋžÍÔöŧĶ10ēĐŖŽ
Ŗ¨1ŖŠ´ōÕÛĪúĘÛēķŖŦĩÚ17ĖėĩÄČÕĪúĘÛÁŋÎĒ________ēĐŖģ
Ŗ¨2ŖŠĮķyĶëxÖŽŧäĩÄē¯ĘũšØĪĩĘŊŖŦ˛ĸĐ´ŗöxĩÄČĄÖĩˇļΧŖģ
Ŗ¨3ŖŠŌŅÖĒČÕĪúĘÛĀûČķ˛ģĩÍĶÚ560ÔĒĩÄĖėĘũš˛ĶĐ6ĖėŖŦÉč´ōÕÛĪúĘÛĩÄÕÛŋÛÎĒaÕÛŖŦĘÔȡļ¨aĩÄ×îĐĄÖĩŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋļÔĶÚÆŊÃæÉĪÁŊĩãAŖŦBŖŦ¸øŗöČįĪÂļ¨ŌåŖēŌÔĩãAģōBÎĒÔ˛ĐÄŖŦABŗ¤ÎĒ°ëžļĩÄÔ˛ŗÆÎĒĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąŖŽČįÍŧÎĒĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąĩÄĘžŌâÍŧŖŽ
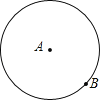
Ŗ¨1ŖŠŌŅÖĒĩãAĩÄ×øąęÎĒŖ¨Ŗ1ŖŦ0ŖŠŖŦĩãBĩÄ×øąęÎĒŖ¨3ŖŦ3ŖŠŖŦÔōĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąĩÄÃæģũÎĒ______Ŗģ
Ŗ¨2ŖŠŌŅÖĒĩãAĩÄ×øąęÎĒŖ¨0ŖŦ0ŖŠŖŦČôÖąĪßyŖŊxŖĢbÉĪÖģ´æÔÚŌģ¸öĩãBŖŦĘšĩÃĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąĩÄÃæģũÎĒ9ĻĐŖŦĮķĩãBĩÄ×øąęŖģ
Ŗ¨3ŖŠŌŅÖĒĩãAÔÚŌÔPŖ¨mŖŦ0ŖŠÎĒÔ˛ĐÄŖŦŌÔ1ÎĒ°ëžļĩÄÔ˛ÉĪŖŦĩãBÔÚÖąĪß![]() ÉĪŖŦČôŌĒĘšËųĶĐĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąĩÄÃæģũļŧ˛ģĐĄĶÚ9ĻĐŖŦÖąŊĶĐ´ŗömĩÄČĄÖĩˇļΧŖŽ
ÉĪŖŦČôŌĒĘšËųĶĐĩãAŖŦBĩÄĄ°Čˇļ¨Ô˛ĄąĩÄÃæģũļŧ˛ģĐĄĶÚ9ĻĐŖŦÖąŊĶĐ´ŗömĩÄČĄÖĩˇļΧŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
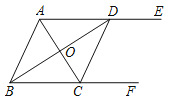
ĄžĖâÄŋĄŋČįÍŧŖŦAEĄÎBFŖŦACÆŊˇÖĄĪBAEŖŦĮŌŊģBFĶÚĩãCŖŦBDÆŊˇÖĄĪABFŖŦĮŌŊģAEĶÚĩãDŖŦÁŦŊĶCDŖŽ
Ŗ¨1ŖŠĮķÖ¤ŖēËÄąßĐÎABCDĘĮÁâĐÎŖģ
Ŗ¨2ŖŠČôĄĪADB=30ĄãŖŦBD=6ŖŦĮķADĩÄŗ¤ŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋČįÍŧŖŦÖąĪß![]() Ķ롴ąČĀũē¯Ęũ
Ķ롴ąČĀũē¯Ęũ![]() ĩÄÍŧĪķĪāŊģĶÚ
ĩÄÍŧĪķĪāŊģĶÚ![]() Ąĸ
Ąĸ![]() ÁŊĩãŖŦšũ
ÁŊĩãŖŦšũ![]() Ąĸ
Ąĸ![]() ÁŊĩãˇÖąđ×÷
ÁŊĩãˇÖąđ×÷![]() ÖáĩÄ´šĪßŖŦ´š×ãˇÖąđÎĒĩã
ÖáĩÄ´šĪßŖŦ´š×ãˇÖąđÎĒĩã![]() Ąĸ
Ąĸ![]() ŖŦÁŦŊĶ
ŖŦÁŦŊĶ![]() Ąĸ
Ąĸ![]() ŖŦÔōËÄąßĐÎ
ŖŦÔōËÄąßĐÎ![]() ĩÄÃæģũÎĒ(ĄĄĄĄ)
ĩÄÃæģũÎĒ(ĄĄĄĄ)
A.4B.8C.12D.24
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
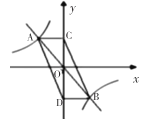
ĄžĖâÄŋĄŋČįÍŧŖŦÔÚžØĐÎABCDÖĐŖŦŌŅÖĒABŖŊ2ŖŦĩãEĘĮBCąßĩÄÖĐĩãŖŦÁŦŊĶAEŖŦĄ÷ABĄäEēÍĄ÷ABEšØĶÚAEËųÔÚÖąĪßļÔŗÆŖŦČôĄ÷BĄäCDĘĮÖąŊĮČũŊĮĐÎŖŦÔōBCąßĩÄŗ¤ÎĒ_____ŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
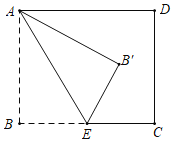
ĄžĖâÄŋĄŋŌģ¸ąČũŊĮ°å°´ČįÍŧËųĘžĩūˇÅÔÚŌģÆđŖŦČôšĖļ¨Ą÷AOBŖŦŊĢĄ÷ACDČÆ×ÅšĢš˛ļĨĩãAŖŦ°´ËŗĘąÕëˇŊĪōĐũ×ĒĻÁļČŖ¨0ĄãŖŧĻÁŖŧ180ĄãŖŠŖŦĩąĄ÷ACDĩÄŌģąßĶëĄ÷AOBĩÄÄŗŌģąßÆŊĐĐĘąŖŦĪāĶĻĩÄĐũ×ĒŊĮĻÁĩÄÖĩĘĮ___.
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖēŗõÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋÉč![]() ĘĮ
ĘĮ![]() ĩÄÆŊžųĘũŖŦŧ´
ĩÄÆŊžųĘũŖŦŧ´![]() ŖŦÔōˇŊ˛î
ŖŦÔōˇŊ˛î![]() ŖŦËüˇ´ĶŗÁËÕâ×éĘũĩIJ¨ļ¯ĐÔŖŦ
ŖŦËüˇ´ĶŗÁËÕâ×éĘũĩIJ¨ļ¯ĐÔŖŦ
Ŗ¨1ŖŠÖ¤Ã÷ŖēļÔČÎŌâĘĩĘũaŖŦx1aŖŦx2aŖŦĄŖŦxnaŖŦĶëx1ŖŦx2ŖŦĄŖŦxn ˇŊ˛îĪāÍŦŖģ
Ŗ¨2ŖŠÖ¤Ã÷![]() Ŗģ
Ŗģ
Ŗ¨3ŖŠŌÔĪÂĘĮÎŌĐŖŗõČũŖ¨1ŖŠ°ā 10 ÎģÍŦŅ§ĩÄÉí¸ßŖ¨ĩĨÎģŖēĀåÃ×ŖŠŖē
169ŖŦ172ŖŦ163ŖŦ173ŖŦ175ŖŦ168ŖŦ170ŖŦ167ŖŦ170ŖŦ171ŖŦŧÆËãÕâ×éĘũĩġŊ˛îŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
šúŧĘŅ§ĐŖĶÅŅĄ - ÁˇĪ°˛áÁĐąí - ĘÔĖâÁĐąí
ēūąąĘĄģĨÁĒÍøÎĨˇ¨ēͲģÁŧĐÅĪĸžŲą¨ÆŊĖ¨ | ÍøÉĪĶĐēĻĐÅĪĸžŲą¨×¨Įø | ĩįĐÅÕŠÆžŲą¨×¨Įø | ÉæĀúʡĐéÎŪÖ÷ŌåĶĐēĻĐÅĪĸžŲą¨×¨Įø | ÉæÆķĮÖȨžŲą¨×¨Įø
ÎĨˇ¨ēͲģÁŧĐÅĪĸžŲą¨ĩįģ°Ŗē027-86699610 žŲą¨ĶĘĪäŖē58377363@163.com