
【题目】如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF,若EF=2![]() ,则矩形的面积为( )
,则矩形的面积为( )
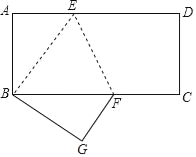
A.32B.28C.30D.36
【答案】A
【解析】
连接BD交EF于O,由折叠的性质可推出BD⊥EF,BO=DO,然后证明△EDO≌△FBO,得到OE=OF,设BC=x,利用勾股定理求BO,再根据△BOF∽△BCD,列出比例式求出x,即可求矩形面积.
解:连接BD交EF于O,如图所示:
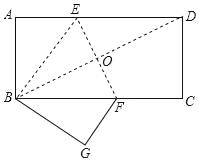
∵折叠纸片使点D与点B重合,折痕为EF,
∴BD⊥EF,BO=DO,
∵四边形ABCD是矩形,
∴AD∥BC
∴∠EDO=∠FBO
在△EDO和△FBO中,
∵∠EDO=∠FBO,DO=BO,∠EOD=∠FOB=90°
∴△EDO≌△FBO(ASA)
∴OE=OF=![]() EF=
EF=![]() ,
,
∵四边形ABCD是矩形,
∴AB=CD=4,∠BCD=90°,
设BC=x,
BD=![]() =
=![]() ,
,
∴BO=![]() ,
,
∵∠BOF=∠C=90°,∠CBD=∠OBF,
∴△BOF∽△BCD,
∴![]() =
=![]() ,
,
即: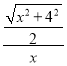 =
=![]() ,
,
解得:x=8,
∴BC=8,
∴S矩形ABCD=ABBC=4×8=32,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 相交于点
相交于点![]() ,线段
,线段![]() 、
、![]() 的长是-元二次方程
的长是-元二次方程![]() 的两根(
的两根(![]() ),
), ![]() ,点
,点![]() 的横坐标为3,反比例函数
的横坐标为3,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)若直线![]() 与反比例函数图象上除点
与反比例函数图象上除点![]() 外的另一交点为
外的另一交点为![]() ,求
,求![]() 的面积:若点
的面积:若点![]() 在
在![]() 轴上,若点
轴上,若点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值:
的最小值:
(2)若点![]() 在坐标轴.上,在平面内存在一点
在坐标轴.上,在平面内存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形且线段
为顶点的四边形是矩形且线段![]() 为矩形的一条边, 直接写出符合条件的
为矩形的一条边, 直接写出符合条件的![]() 点坐标.
点坐标.
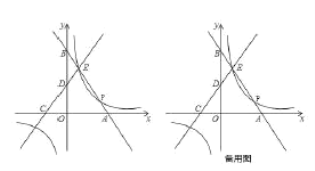
查看答案和解析>>
科目:初中数学 来源: 题型:
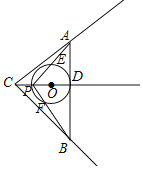
【题目】如图,在△ABC中,AB=7,BC=4![]() ,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
(1)求sin∠ACD的值.
(2)在点P的整个运动过程中:
①当⊙O与射线CA相切时,求出所有满足条件时x的值;
②当x为何值时,四边形DEPF为矩形,并求出矩形DEPF的面积.
(3)如果将△ADC绕点D顺时针旋转150°,得△A′DC′,若点A′和点C′有且只有一个点在圆内,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校![]() 名同学对学校设置的体操、篮球、足球、跑步、舞蹈等课外活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图(均不完整),请回答下列问题.
名同学对学校设置的体操、篮球、足球、跑步、舞蹈等课外活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图(均不完整),请回答下列问题.
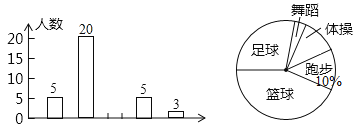
(1)在这次问卷调查中,共抽查了_________名同学;
(2)补全条形统计图;
(3)估计该校![]() 名同学中喜爱足球活动的人数;
名同学中喜爱足球活动的人数;
(4)在体操社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加体操大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着私家车的增多,“停车难”成了很多小区的棘手问题.某小区为解决这个问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中,入口处斜坡![]() 的坡角为
的坡角为![]() ,水平线
,水平线![]() .根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到
.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点![]() 在第一象限内,连接
在第一象限内,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的而积为S,求S与
的而积为S,求S与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
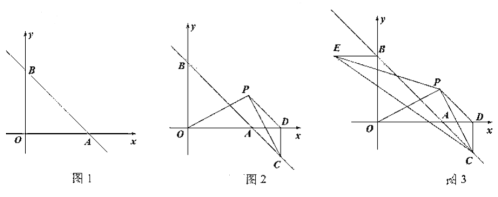
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为_____.
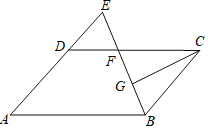
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西南大学附中一年一度的“缤纷节”受到社会各界的高度赞扬,2018年12月14日西南大学附中成功举办了第十八届缤纷节,为成功筹办此次缤纷节,学校后勤工作人员进行了繁琐细致地准备工作,为了搭建舞台、后勤服务平台和安排全校师生及家长朋友们的座位,学校需要购买钢材1380根,购买胶板凳2300个.现安排A,B两种型号的货车共10辆运往学校,已知一辆A型货车可以用150根钢材和200个板凳装满,一辆B型货车可以用120根钢材和350个板凳装满,并且一辆A型货车的运费为500元,一辆B型货车的运费为520元;设运输钢材和板凳的总费用为y元,租用A型货车x辆.
(1)试写出y与x之间的函数关系式,并写出x的取值范围;
(2)按要求有哪几种运输方案,运费最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已如如图1,在平面直角坐标系中,点A的坐标为(6,0)、点B的坐标为(0,8),点C在y轴上,作直线AC.点B关于直线AC的对称点B′刚好在x轴上,连接CB′.
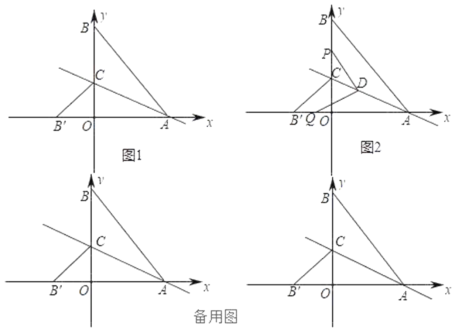
(1)写出点B′的坐标,并求出直线AC对应的函数表达式;
(2)点D在线段AC上,连接DB、DB′、BB′,当△DBB′是等腰直角三角形时,求点D坐标;
(3)如图2,在(2)的条件下,点P从点B出发以每秒2个单位长度的速度向原点O运动,到达点O时停止运动,连接PD,过D作DP的垂线,交x轴于点Q,问点P运动几秒时△ADQ是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com