
【题目】西南大学附中一年一度的“缤纷节”受到社会各界的高度赞扬,2018年12月14日西南大学附中成功举办了第十八届缤纷节,为成功筹办此次缤纷节,学校后勤工作人员进行了繁琐细致地准备工作,为了搭建舞台、后勤服务平台和安排全校师生及家长朋友们的座位,学校需要购买钢材1380根,购买胶板凳2300个.现安排A,B两种型号的货车共10辆运往学校,已知一辆A型货车可以用150根钢材和200个板凳装满,一辆B型货车可以用120根钢材和350个板凳装满,并且一辆A型货车的运费为500元,一辆B型货车的运费为520元;设运输钢材和板凳的总费用为y元,租用A型货车x辆.
(1)试写出y与x之间的函数关系式,并写出x的取值范围;
(2)按要求有哪几种运输方案,运费最少为多少元?
【答案】(1)y=﹣20x+5200,6≤x≤8;(2)有以下三种运输方案:①A型货车6辆,B型货车4辆;②A型货车7辆,B型货车3辆;③A型货车8辆,B型货车2辆.运费最少为5040元
【解析】
(1)根据题意表示出两种车的费用的和就是总费用;
(2)根据题意建立不等式组,求出x的取值范围,根据取值范围,列出所有可能的方案,再根据一次函数的性质解答即可.
解:(1)根据题意,得y=500x+520(10﹣x)=﹣20x+5200;
即y=﹣20x+5200;
(2)由题意得
![]() ,
,
解得6≤x≤8,
又∵x为正整数,
∴x=6,7,8,
∴10﹣x=4,3,2.
∴有以下三种运输方案:
①A型货车6辆,B型货车4辆;
②A型货车7辆,B型货车3辆;
③A型货车8辆,B型货车2辆.
∵y=﹣20x+5200,k=﹣20<0,y随x的增大而减小,
∴方案③运费最少.
最少运费为:y=﹣20×8+5200=5040.
答:有三种运输方案,运费最少为5040元.


科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
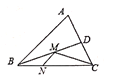
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.
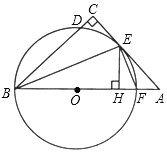
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=13,点A、B的坐标分别为(1,0),(6,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣4上时,线段BC扫过的面积为( )

A.84B.80C.91D.78
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放假时小华父子俩一同出发去露营,步行途中小华发现睡袋忘拿了跑步回家取,之后立刻返程跑步追赶爸爸,期间爸爸继续步行去往露营地,会合时爸爸发现还需要探照灯,为节约时间爸爸乘车回家去拿,小华继续步行至露营地,爸爸拿到探照灯后乘车也到了终点(假定步行、跑步和汽车均为匀速,且二人取物品时间忽略不计),二人之间的距离s(米)与他们出发时间t(分钟)之间的关系如图所示,则当爸爸到家时,小华与露营地相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() 与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣
与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣![]() x平行,且与直线l1相交于点B,与x轴交于点C.
x平行,且与直线l1相交于点B,与x轴交于点C.

(1)求点C坐标;
(2)若点P是y轴右侧直线l1上一动点,点Q是直线l2上一动点,点D(﹣2![]() ,6
,6![]() ),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
(3)将△AOB沿着直线l2平移,平移后记为△A1O1B1,直线O1B1交11于点M,直线A1B1交x轴于点N,当△B1MN是等腰三角形时,求点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市教育局在全市中小学推广某学校“品格教育”科研成果,其中“敬老孝亲”是“品格教育”亮点之一. 重阳节(农历九月初九)快到了,某校八年级(1)班班委发起为老人们献上真挚的节日祝福活动,决定全班同学利用课余时间去卖鲜花筹集慰问金.已知同学们从花店按每支1.5元买进鲜花,并按每支4.5元卖出.
(1)求同学们卖出鲜花的销售额![]() (元)与销售量
(元)与销售量![]() (支)之间的函数关系式;
(支)之间的函数关系式;
(2)若从花店购买鲜花的同时,还总共用去40元购买包装材料,求所筹集的慰问金![]() (元)与销售量
(元)与销售量![]() (支)之间的函数关系式;若要筹集不少于500元的慰问金,则至少要卖出鲜花多少支?(慰问金 = 销售额 - 成本)
(支)之间的函数关系式;若要筹集不少于500元的慰问金,则至少要卖出鲜花多少支?(慰问金 = 销售额 - 成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,分别交正比例函数的图象于点
轴的垂线,分别交正比例函数的图象于点![]() ,交一次函数的图象于点
,交一次函数的图象于点![]() ,连接
,连接![]() .
.

(1)求这两个函数的表达式;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 为直角三角形?若存在,请直接写出满足条件的所有
为直角三角形?若存在,请直接写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AB=6,sin∠BAC=![]()
(1)BC长=_____;
(2)若点P是线段AC上一点,当△PCD是等腰三角形时,求AP的长;
(3)如图(2),点E是边BC上一点,且PE⊥PD.则:①![]() =_____;
=_____;
②如图(3)分别以PE、PD为边作矩形PEFD,若AP=2![]() ,求CF的长.
,求CF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com