
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.
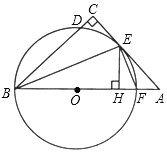
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
【答案】详见解析.
【解析】
(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;
(2)∠C=∠BHE=90°,∠EBC=∠EBA,∠BEC=∠BEH,根据BF是⊙O是直径,
得到∠BEF=90°,∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,得到∠FEH=∠FEA,
即可证明FE平分∠AEH.
(3)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF.
(1)证明:(1)如图,连接OE.
∵BE⊥EF,∴∠BEF=90°,
∴BF是圆O的直径,
∴OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,
∴∠BEC=∠BEH,
∵BF是⊙O是直径,
∴∠BEF=90°,
∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,
∴∠FEH=∠FEA,
∴FE平分∠AEH.
(3)证明:如图,连结DE.
∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE,
∵∠C=∠EHF=90°,
∴△CDE≌△HFE(AAS),
∴CD=HF,


科目:初中数学 来源: 题型:
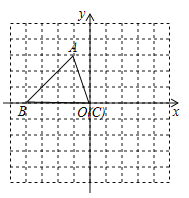
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在铁路线![]() 附近有两个村庄
附近有两个村庄![]() ,到铁路的距离分别是
,到铁路的距离分别是![]() 和
和![]() ,作
,作![]() ,垂足分别为
,垂足分别为![]() ,且
,且![]() 现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
(1)请利用尺规作图确定站![]() 的位置.(不写作法,保留作图痕迹)
的位置.(不写作法,保留作图痕迹)
(2)求出![]() 长度.
长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进 A、B 两种艺术节纪念品,若购进 A 种纪念品 8 件,B 种纪念品 3 件,需要 950 元;若购进A 种纪念品 5 件,B 种纪念品 6 件,需要 800 元.
(1)求购进A、B 两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共 100 件,考虑市场需求和资金周转,用于购买这 100 件纪念品的资金不少于 7000 元,但不超过 7500 元,那么该商店共有几种进货方案?
(3)若销售每件 A 件纪念品可获利润 20 元,每件 B 种纪念品可获利润 30 元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图像,图1是产品销售量y(件)与时间t(天)的函数关系,图2是一件产品的销售利润z(元)与时间t(天)的函数关系,已知日销售利润=日销售量×每件产品的销售利润,下列结论错误的是( )。
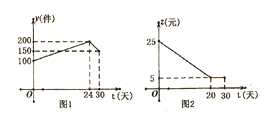
A. 第24天的销售量为200件B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=56°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕点P旋转时,下列结论①EF=AP;②△EPF为等腰直角三角形;③AE=CF;④S四边形AEPF![]() ,正确的有( )
,正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西南大学附中一年一度的“缤纷节”受到社会各界的高度赞扬,2018年12月14日西南大学附中成功举办了第十八届缤纷节,为成功筹办此次缤纷节,学校后勤工作人员进行了繁琐细致地准备工作,为了搭建舞台、后勤服务平台和安排全校师生及家长朋友们的座位,学校需要购买钢材1380根,购买胶板凳2300个.现安排A,B两种型号的货车共10辆运往学校,已知一辆A型货车可以用150根钢材和200个板凳装满,一辆B型货车可以用120根钢材和350个板凳装满,并且一辆A型货车的运费为500元,一辆B型货车的运费为520元;设运输钢材和板凳的总费用为y元,租用A型货车x辆.
(1)试写出y与x之间的函数关系式,并写出x的取值范围;
(2)按要求有哪几种运输方案,运费最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】积极响应市委市政府“加快建设绿水青山的美丽乐山”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图所示两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为______;
(2)请将条形和扇形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民2万人,请你估计这2万人中最喜欢玉兰树的有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com