练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠AOB＝56°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为________________．

    【答案】124°或76°或28°

    【解析】

    题目要求∠OEC的度数，而没有告诉∠OEC是等腰△OCE的顶角还是底角，由此此题要分类讨论;由角平分线的定义先求出∠AOC的度数，再分OE=CE、OC=CE、OE=OC进行讨论，结合等腰三角形的性质和三角形的内角和定理即可求出∠OEC的度数.

    ∵∠AOB=56°，0C平分∠AOB,

    ∴∠AOC=28°,

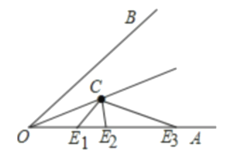
    ①当E在时，OE=CE,

    ∵∠AOC=∠OCE=28°

    ∴∠OEC'=180°-28°-28°=124°，

    ②当E在点时，OC=OE,可得：

    ③当E在时，OC'=CE,

    则∠OEC=∠A0C=28°,

    故答案为: 124°或76°或28°.

    【点睛]

    本题考查等腰三角形内角的题目，解决本题的关键是结合等腰三角形的性质和三角形内角和定理解答.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

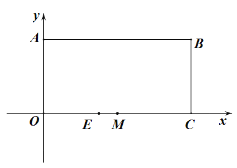
    【题目】如图，矩形OABC的顶点A的坐标（0,4），C的坐标为（8,0），把矩形折叠，使点C与点A重合，折痕为DE．

    求出点E的坐标．

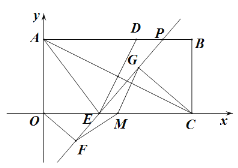
    （2）点M为OC的中点，点P为线段AB上一动点，作直线EP，分别过点O、C作直线EP的垂线，垂足分别为点F、G．求证：MF=MG

    （3）在（2）的条件下，当△FMG为等腰直角三角形时，请直接写出此时直线EP的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点在第一象限，且，点的坐标为，设的面积为，

    (1)当点的横坐标为1时，试求的面积.

    (2)求S关于x的函数表达式及自变量x的取值范围.

    (3)试判断的面积能否大于6，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“全民读书月”活动中，小明调查了班级里40名同学本学期计划购买课外书的花费情况，并将结果绘制成如图所示的统计图，请根据相关信息，解答下列问题：（直接填写结果）

    （1）本次调查获取的样本数据的众数是 ；

    （2）这次调查获取的样本数据的中位数是 ；

    （3）若该校共有学生1000人，根据样本数据，估计本学期计划购买课外书花费50元的学生有 人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，∠ABC的平分线BE交AC于点E，过点E作直线BE的垂线交AB于点F，⊙O是△BEF的外接圆．

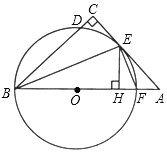
    （1）求证：AC是⊙O的切线；

    （2）过点E作EH⊥AB于点H，求证：EF平分∠AEH；

    （3）求证：CD=HF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某计算机中有、、三个按键，以下是这三个按键的功能．

    (1)．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．

    (2)．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下后会变成0.04．

    (3)．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下后会变成36．

    若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按，之后以、、的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（　　）

    A. 0.01 B. 0.1 C. 10 D. 100

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把Rt△ABC放在平面直角坐标系内，其中∠CAB＝90°，BC＝13，点A、B的坐标分别为（1，0），（6，0），将△ABC沿x轴向右平移，当点C落在直线y＝2x﹣4上时，线段BC扫过的面积为（　　）

    A.84B.80C.91D.78

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：y＝与x轴、y轴分别相交于点A、B，直线l2与直线y＝﹣x平行，且与直线l1相交于点B，与x轴交于点C．

    （1）求点C坐标；

    （2）若点P是y轴右侧直线l1上一动点，点Q是直线l2上一动点，点D（﹣2，6），求当S△PBC＝S四边形AOBD时，点P的坐标，并求出此时，PQ+DQ的最小值；

    （3）将△AOB沿着直线l2平移，平移后记为△A1O1B1，直线O1B1交11于点M，直线A1B1交x轴于点N，当△B1MN是等腰三角形时，求点A1的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，是外一点，，分别和切于，两点，是上任意一点，过作的切线分别交，于，．

    若的周长为，则的长为________；

    连接、，若，则的度数为________度．

    查看答案和解析>>

    同步练习册答案