
【题目】点![]() 在第一象限,且
在第一象限,且![]() ,点
,点![]() 的坐标为
的坐标为![]() ,设
,设![]() 的面积为
的面积为![]() ,
,
(1)当点![]() 的横坐标为1时,试求
的横坐标为1时,试求![]() 的面积.
的面积.
(2)求S关于x的函数表达式及自变量x的取值范围.
(3)试判断![]() 的面积能否大于6,并说明理由.
的面积能否大于6,并说明理由.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5; 5,12,13; 7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且勾为3时,股![]() ,弦
,弦![]() ;勾为5时,股
;勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24=__________;弦25=___________.
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股=________;弦=_______.
的式子表示股和弦,则股=________;弦=_______.
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用![]() (
(![]() 为偶数且
为偶数且![]() )的代数式来表示直角三角形的另一条直角边和弦的长.
)的代数式来表示直角三角形的另一条直角边和弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
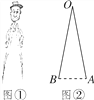
【题目】如图①是一副创意卡通圆规,图②是其平面示意图,OA是支撑臂,OB是旋转臂.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径(结果精确到0.01cm);
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度(结果精确到0.01cm,参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在铁路线![]() 附近有两个村庄
附近有两个村庄![]() ,到铁路的距离分别是
,到铁路的距离分别是![]() 和
和![]() ,作
,作![]() ,垂足分别为
,垂足分别为![]() ,且
,且![]() 现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
(1)请利用尺规作图确定站![]() 的位置.(不写作法,保留作图痕迹)
的位置.(不写作法,保留作图痕迹)
(2)求出![]() 长度.
长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=3cm,BC=5cm,AE=![]() AB,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△BEP为等腰三角形?
AB,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△BEP为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进 A、B 两种艺术节纪念品,若购进 A 种纪念品 8 件,B 种纪念品 3 件,需要 950 元;若购进A 种纪念品 5 件,B 种纪念品 6 件,需要 800 元.
(1)求购进A、B 两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共 100 件,考虑市场需求和资金周转,用于购买这 100 件纪念品的资金不少于 7000 元,但不超过 7500 元,那么该商店共有几种进货方案?
(3)若销售每件 A 件纪念品可获利润 20 元,每件 B 种纪念品可获利润 30 元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=56°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代称直角三角形为“勾股形”,并且直角边中较短边为勾,另一直角边为股,斜边为弦.如图1所示,数学家刘徽(约公元225年—公元295年)将勾股形分割成一个正方形和两对全等的直角三角形,后人借助这种分割方法所得的图形证明了勾股定理.如图2所示的长方形,是由两个完全相同的“勾股形”拼接而成,若![]() ,
,![]() ,则长方形的面积为______.
,则长方形的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com