
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

【答案】(1)∠EAD的余切值为![]() ;(2)
;(2)![]() =
=![]() .
.
【解析】
(1)在Rt△ADB中,根据AB=13,cos∠BAC=![]() ,求出AD的长,由勾股定理求出BD的长,进而可求出DE的长,然后根据余切的定义求∠EAD的余切即可;
,求出AD的长,由勾股定理求出BD的长,进而可求出DE的长,然后根据余切的定义求∠EAD的余切即可;
(2)过D作DG∥AF交BC于G,由平行线分线段成比例定理可得CD:AD=CG:FG=3:5,从而可设CD=3x,AD=5x,再由EF∥DG,BE=ED, 可知BF=FG=5x,然后可求BF:CF的值.
(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=![]() ,
,
∴AD=5, 由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切=![]() =
=![]() ;
;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5, ∴CD=3,
∵DG∥AF,
∴![]() =
=![]() ,
,
设CD=3x,AD=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合.若∠CEF=50°,则∠AOF的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
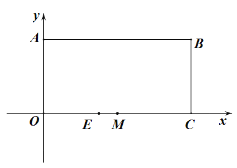
【题目】如图,矩形OABC的顶点A的坐标(0,4),C的坐标为(8,0),把矩形折叠,使点C与点A重合,折痕为DE.
求出点E的坐标.
(2)点M为OC的中点,点P为线段AB上一动点,作直线EP,分别过点O、C作直线EP的垂线,垂足分别为点F、G.求证:MF=MG
(3)在(2)的条件下,当△FMG为等腰直角三角形时,请直接写出此时直线EP的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
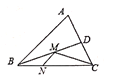
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
60≤m<70 | 38 | 0.38 |
70≤m<80 | a | 0.32 |
80≤m<90 | b | c |
90≤m≤100 | 10 | 0.1 |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是_____;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在第一象限,且
在第一象限,且![]() ,点
,点![]() 的坐标为
的坐标为![]() ,设
,设![]() 的面积为
的面积为![]() ,
,
(1)当点![]() 的横坐标为1时,试求
的横坐标为1时,试求![]() 的面积.
的面积.
(2)求S关于x的函数表达式及自变量x的取值范围.
(3)试判断![]() 的面积能否大于6,并说明理由.
的面积能否大于6,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() 与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣
与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣![]() x平行,且与直线l1相交于点B,与x轴交于点C.
x平行,且与直线l1相交于点B,与x轴交于点C.

(1)求点C坐标;
(2)若点P是y轴右侧直线l1上一动点,点Q是直线l2上一动点,点D(﹣2![]() ,6
,6![]() ),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
(3)将△AOB沿着直线l2平移,平移后记为△A1O1B1,直线O1B1交11于点M,直线A1B1交x轴于点N,当△B1MN是等腰三角形时,求点A1的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com