
【题目】如图,在等腰△ABC中,AB=AC,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合.若∠CEF=50°,则∠AOF的度数是_____.

【答案】105°
【解析】
由折叠的性质可得OE=CE,∠CEF=∠OEF=50°,OF=FC,可求∠OCE=∠COE=40°,由等腰三角形的性质和线段垂直平分线的性质可求OAB=∠OBA=∠OAC=∠OCA=25°,由三角形内角和定理可求∠AOC=130°,即可求∠AOF的度数.
如图,连接OB,

∵点C与点O恰好重合,
∴OE=CE,∠CEF=∠OEF=50°,OF=FC,
∴∠OCE=∠COE=40°
∵AB=AC,AO平分∠BAC,
∴AO是BC的垂直平分线,∠OAB=∠OAC,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴AO=BO=CO,
∴∠OBC=∠OCB=40°,∠OAB=∠OBA=∠OAC=∠OCA,
∵∠OAB+∠OAC+∠ABO+∠ACO+∠OBC+∠OCB=180°
∴∠OAB=∠OBA=∠OAC=∠OCA=25°,
∵OF=FC
∴∠FOC=∠ACO=25°
在△AOC中,∠AOC=180°﹣∠OAC﹣∠OCA=130°
∴∠AOF=∠AOC﹣∠FOC=130°﹣25°=105°
故答案为:105°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
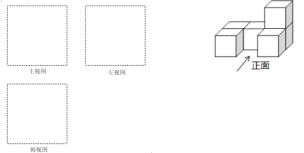
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
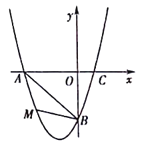
【题目】在平面直角坐标系中,已知抛物线经过A(-3,0),B(0,-3),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S
关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
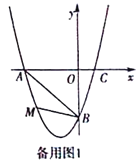
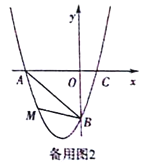
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图是三个方向看到的一个几何体的形状.
(1)写出这个几何体的名称;
(2)写出它的侧面展开的形状;
(3)若从正面看到的高为10cm,从上面看到的三角形的三边长都为4cm,求这个几何体的侧面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5; 5,12,13; 7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且勾为3时,股![]() ,弦
,弦![]() ;勾为5时,股
;勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24=__________;弦25=___________.
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股=________;弦=_______.
的式子表示股和弦,则股=________;弦=_______.
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用![]() (
(![]() 为偶数且
为偶数且![]() )的代数式来表示直角三角形的另一条直角边和弦的长.
)的代数式来表示直角三角形的另一条直角边和弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;

归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
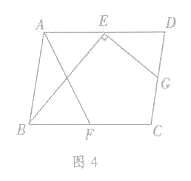
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com