
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=![]() 时,a= ,b= ;
时,a= ,b= ;
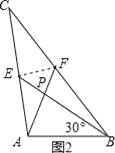
如图2,当∠ABE=30°,c=4时,a= ,b= ;

归纳证明
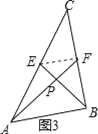
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
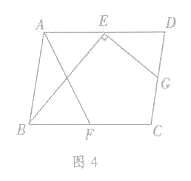
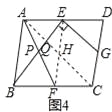
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
【答案】(1)2![]() ,2
,2![]() ;2
;2![]() ,2
,2![]() ;(2)
;(2)![]() +
+![]() =5
=5![]() ;(3)AF=4.
;(3)AF=4.
【解析】
试题(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=![]() AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=
AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=![]() AB=
AB=![]() ,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=
,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=![]() =
=![]() ,∴AC=BC=2
,∴AC=BC=2![]() ,∴a=b=2
,∴a=b=2![]() ,如图2,连接EF,同理可得:EF=
,如图2,连接EF,同理可得:EF=![]() ×4=2,∵EF∥AB,∴△PEF~△ABP,∴
×4=2,∵EF∥AB,∴△PEF~△ABP,∴![]() ,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2
,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2![]() ,∴PF=1,PE=
,∴PF=1,PE=![]() ,在Rt△APE和Rt△BPF中,AE=
,在Rt△APE和Rt△BPF中,AE=![]() ,BF=
,BF=![]() ,∴a=2
,∴a=2![]() ,b=2
,b=2![]() ,故答案为:2
,故答案为:2![]() ,2
,2![]() ,2
,2![]() ,2
,2![]() ;
;
(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=![]() PA=
PA=![]() ,PE=
,PE=![]() =
=![]() ,AE2=AP2+PE2=c2sin2α+
,AE2=AP2+PE2=c2sin2α+![]() ,BF2=PB2+PF2=
,BF2=PB2+PF2=![]() +c2cos2α,∴
+c2cos2α,∴![]() =c2sin2α+
=c2sin2α+![]() ,
,![]() =
=![]() +c2cos2α,∴
+c2cos2α,∴![]() +
+![]() =
=![]() +c2cos2α+c2sin2α+
+c2cos2α+c2sin2α+![]() ,∴a2+b2=5c2;
,∴a2+b2=5c2;
(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2![]() ,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=
,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=![]() AD,BF=
AD,BF=![]() BC,∴AE=BF=CF=
BC,∴AE=BF=CF=![]() AD=
AD=![]() ,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,
,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,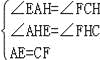 ,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5
,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5![]() ﹣EF2=16,∴AF=4.
﹣EF2=16,∴AF=4.


科目:初中数学 来源: 题型:
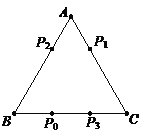
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合.若∠CEF=50°,则∠AOF的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=﹣2x+b与反比例函数y=![]() 交于点A、B,与x轴交于点C.
交于点A、B,与x轴交于点C.
(1)若A(﹣3,m)、B(1,n).直接写出不等式﹣2x+b>![]() 的解.
的解.
(2)求sin∠OCB的值.
(3)若CB﹣CA=5,求直线AB的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点.点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
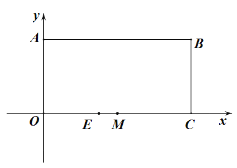
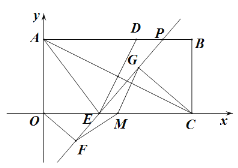
【题目】如图,矩形OABC的顶点A的坐标(0,4),C的坐标为(8,0),把矩形折叠,使点C与点A重合,折痕为DE.
求出点E的坐标.
(2)点M为OC的中点,点P为线段AB上一动点,作直线EP,分别过点O、C作直线EP的垂线,垂足分别为点F、G.求证:MF=MG
(3)在(2)的条件下,当△FMG为等腰直角三角形时,请直接写出此时直线EP的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com