
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
【答案】(1)甲型机器人每小时分类80kg垃圾。则乙型机器人每小时分类60kg垃圾;(2)甲型机器人退出后乙型机器人还需要工作7小时
【解析】
(1)根据甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等列出方程求解即可;
(2)根据(1)求得的答案通过计算即可求得答案.
(1)解:设甲型机器人每小时分类![]() 垃圾。则乙型机器人每小时分类
垃圾。则乙型机器人每小时分类![]() 垃圾,
垃圾,
由题意得: ![]()
解得:![]()
检验:当![]() 时,
时,![]() ,
,
所以,原分式方程的解为![]() ,
,
![]()
答:甲型机器人每小时分类![]() 垃圾。则乙型机器人每小时分类
垃圾。则乙型机器人每小时分类![]() 垃圾;
垃圾;
(2)[700-(80+60)×2]÷60=7小时
答:甲型机器人退出后乙型机器人还需要工作7小时.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】某品牌T恤专营批发店的T恤衫在进价基础上加价m%销售,每月销售额9万元,该店每月固定支出1.7万元,进货时还需付进价5%的其它费用.
(1)为保证每月有1万元的利润,m的最小值是多少?(月利润=总销售额-总进价-固定支
出-其它费用)
(2)经市场调研发现,售价每降低1%,销售量将提高6%,该店决定自下月起降价以促进销售,已知每件T恤原销售价为60元,问:在m取(1)中的最小值且所进T恤当月能够全部销售完的情况下,销售价调整为多少时能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 关于
关于![]() 的二次函数
的二次函数![]()
(1)当![]() 时,求该函数图像的顶点坐标.
时,求该函数图像的顶点坐标.
(2)在(1)条件下,![]() 为该函数图像上的一点,若
为该函数图像上的一点,若![]() 关于原点的对称点
关于原点的对称点![]() 也落在该函数图像上,求
也落在该函数图像上,求![]() 的值
的值
(3)当函数的图像经过点(1,0)时,若![]() 是该函数图像上的两点,试比较
是该函数图像上的两点,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.
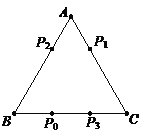
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。
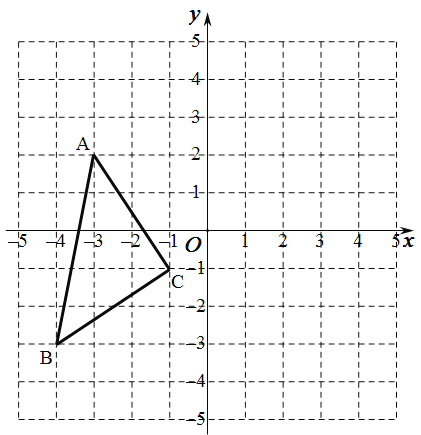
(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 2 | 3 | 10 | … |
日销售量(n件) | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格-每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合.若∠CEF=50°,则∠AOF的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A的坐标(0,4),C的坐标为(8,0),把矩形折叠,使点C与点A重合,折痕为DE.
求出点E的坐标.
(2)点M为OC的中点,点P为线段AB上一动点,作直线EP,分别过点O、C作直线EP的垂线,垂足分别为点F、G.求证:MF=MG
(3)在(2)的条件下,当△FMG为等腰直角三角形时,请直接写出此时直线EP的表达式.
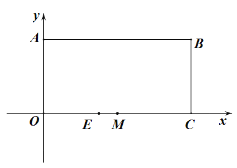
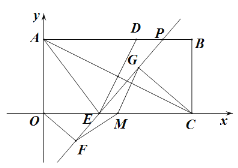
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com