
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 2 | 3 | 10 | … |
日销售量(n件) | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格-每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
【答案】(1)180件;(2)第40天,利润最大7200元;(3)46天
【解析】试题(1)根据待定系数法解出一次函数解析式,然后把x=10代入即可;
(2)设利润为y元,则当1≤x<50时,y=﹣2x2+160x+4000;当50≤x≤90时,y=﹣120x+12000,分别求出各段上的最大值,比较即可得到结论;
(3)直接写出在该产品销售的过程中,共有46天销售利润不低于5400元.
试题解析:解:(1)∵n与x成一次函数,∴设n=kx+b,将x=1,m=198,x=3,m=194代入,得: ![]() , 解得:
, 解得: ![]() ,
,
所以n关于x的一次函数表达式为n=-2x+200;
当x=10时,n=-2×10+200=180.
(2)设销售该产品每天利润为y元,y关于x的函数表达式为: ![]()
当1≤x<50时,y=-2x2+160x+4000=-2(x-40)2+7200,
∵-2<0,∴当x=40时,y有最大值,最大值是7200;
当50≤x≤90时,y=-120x+12000,
∵-120<0,∴y随x增大而减小,即当x=50时,y的值最大,最大值是6000;
综上所述:当x=40时,y的值最大,最大值是7200,即在90天内该产品第40天的销售利润最大,最大利润是7200元;
(3)在该产品销售的过程中,共有46天销售利润不低于5400元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.

(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①所示),使![]() .
.
(2)摆放成如图②的四边形,则这时窗框的形状是平行四边形,它的依据是____________.
(3)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是矩形,它的依据是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
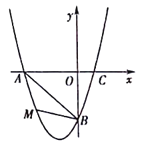
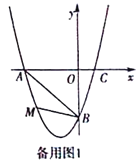
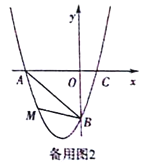
【题目】在平面直角坐标系中,已知抛物线经过A(-3,0),B(0,-3),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S
关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图是三个方向看到的一个几何体的形状.
(1)写出这个几何体的名称;
(2)写出它的侧面展开的形状;
(3)若从正面看到的高为10cm,从上面看到的三角形的三边长都为4cm,求这个几何体的侧面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5; 5,12,13; 7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且勾为3时,股![]() ,弦
,弦![]() ;勾为5时,股
;勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24=__________;弦25=___________.
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股=________;弦=_______.
的式子表示股和弦,则股=________;弦=_______.
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用![]() (
(![]() 为偶数且
为偶数且![]() )的代数式来表示直角三角形的另一条直角边和弦的长.
)的代数式来表示直角三角形的另一条直角边和弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
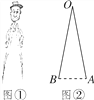
【题目】如图①是一副创意卡通圆规,图②是其平面示意图,OA是支撑臂,OB是旋转臂.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径(结果精确到0.01cm);
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度(结果精确到0.01cm,参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com