
����Ŀ���Ķ����ϣ���ѧ���ϣ�����ʦ�������ʽx2��4x+5����Сֵʱ�����ù�ʽa2��2ab+b2=��a��b��2����ʽ�������±��Σ�x2��4x+5=x2��4x+4+1=��x��2��2+1��
����x��2��2��0��
���ԣ�x��2��2+1��1��
��x=2ʱ����x��2��2+1=1��
��ˣ�x��2��2+1����Сֵ1����x2��4x+5����СֵΪ1��
ͨ���Ķ������������⣺
��1������ʽx2+6x+12����СֵΪ�� ����
��2�������ʽ��x2+2x+9��������Сֵ��
��3���ԱȽϴ���ʽ3x2��2x��2x2+3x��7�Ĵ�С����˵�����ɣ�
���𰸡�(1)3;(2) ��x2+2x+9���ֵΪ10;(3) 3x2��2x��2x2+3x��7�����ɼ�����
��������
��1������2�����շ����Ľ��ⷽ�����з�����ɣ�
��2���������������ʽ�IJ���÷����еķ����ж����ò��ֵ���������ɵõ���������ʽ�Ĵ�С��ϵ.
��1����x2+6x+12=��x+3��2+3����![]() ��
��
��![]() ��������ʽx2+6x+12����СֵΪ3��
��������ʽx2+6x+12����СֵΪ3��
��2������x2+2x+9=����x��1��2+10������x��1��2��0��
�ੁ��x��1��2��0��
��![]() ��������ʽ��x2+2x+9�����ֵΪ10��
��������ʽ��x2+2x+9�����ֵΪ10��
��3������3x2��2x������2x2+3x��7��=x2��5x+7=![]() ����
����![]() ��
��
��![]() ��
��
��3x2��2x��2x2+3x��7��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꣬�������ϰ���������һ��ũ����ջ�����20�֣�����12�֣��ּƻ����üס������ֻ�����8��������ˮ��ȫ������������ۣ���֪һ�����ֻ�����װ����4�ֺ�����1�֣�һ�����ֻ�����װ���˺����Ӹ�2��.��Ӱ��żס������ֻ���һ���Եؽ�ˮ���˵����۵صķ������У� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��ODƽ�֡�BOE��OFƽ�֡�AOE
��1���ж�OF��OD��λ�ù�ϵ��������֤����
��2������AOC����AOD��1��5�����EOF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������һ�ֽ�����Ʒ���г����ܵ��ձ黶ӭ��ÿ����ڹ��ڡ������г���ȫ�����꣮�ù�˾�������Ϊ6000�������ڹ����г����ۣ�ƽ��ÿ����Ʒ�����������������![]() �Ĺ�ϵ���±���
�Ĺ�ϵ���±���
������ |
|
|
��������Ԫ�� |
|
|
���ڹ������ۣ�ƽ��ÿ����Ʒ��������������������![]() �Ĺ�ϵ���±���
�Ĺ�ϵ���±���
������ |
|
|
��������Ԫ�� | 100 |
|
��1����![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() Ϊ��
��![]() =��
=��
��2���ù�˾ÿ����ڡ��������������Ϊ����ʱ����ʹ��˾ÿ���������Ϊ60��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ������ѧ�������蹺��![]() ���ֽ�Ʒ��160��������
���ֽ�Ʒ��160��������![]() �ֽ�Ʒ�ĵ���Ϊ12Ԫ��
�ֽ�Ʒ�ĵ���Ϊ12Ԫ��![]() �ֽ�Ʒ�ĵ���Ϊ8Ԫ���ҹ���
�ֽ�Ʒ�ĵ���Ϊ8Ԫ���ҹ���![]() �ֽ�Ʒ������������
�ֽ�Ʒ������������![]() �ֽ�Ʒ������3�������蹺��
�ֽ�Ʒ������3�������蹺��![]() �ֽ�Ʒ������Ϊ
�ֽ�Ʒ������Ϊ![]() ��.
��.
��1������������գ�
����![]() �ֽ�Ʒ�ķ���Ϊ___��Ԫ����
�ֽ�Ʒ�ķ���Ϊ___��Ԫ����
����![]() �ֽ�Ʒ�ķ���Ϊ___��Ԫ����
�ֽ�Ʒ�ķ���Ϊ___��Ԫ����
��2�����������ֽ�Ʒ������ܷ���Ϊ![]() Ԫ������
Ԫ������![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���ֽ�Ʒ��������ټ�ʱ������ܷ������٣���������ٷ���.
���ֽ�Ʒ��������ټ�ʱ������ܷ������٣���������ٷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
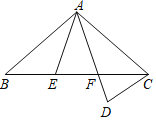
����Ŀ����ͼ����ABC�У�AB=AC����E��F�ڱ�BC�ϣ�BE=CF����D��AF���ӳ����ϣ�AD=AC��
��1����֤����ABE�ա�ACF��
��2������BAE=30�������ADC=�� ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,��1=��2,GΪAD���е�,�ӳ�BG��AC��E�� FΪAB�ϵ�һ��,CF��AD��H�������ж���ȷ����( )

A.AD�ǡ�ABE�Ľ�ƽ����B.BE�ǡ�ABD��AD�ϵ�����
C.AHΪ��ABC�Ľ�ƽ����D.CHΪ��ACD��AD�ϵĸ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У� �Խ���AC��BD�ཻ�ڵ�O. E��F�ǶԽ���AC�ϵ�������ͬ�㣬��E��F����������������ʱ���ı���DEBF��һ����ƽ���ı���( ).
ABCD�У� �Խ���AC��BD�ཻ�ڵ�O. E��F�ǶԽ���AC�ϵ�������ͬ�㣬��E��F����������������ʱ���ı���DEBF��һ����ƽ���ı���( ).

A.AE��CFB.DE��BFC.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC����BAC=90����ֱ����EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F������EPF����ABC���ƶ���P��תʱ����E����A��B�غϣ������������ĸ����ۣ���AE=CF���ڡ�EPF�ǵ���ֱ�������Σ���2S�ı���AEPF=S��ABC����BE+CF=EF������������ʼ����ȷ���У�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com