
【题目】某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6000件,若在国内市场销售,平均每件产品的利润与国内销售量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) |
|
|
若在国外销售,平均每件产品的利润与国外的销售数量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) | 100 |
|
(1)用![]() 的代数式表示
的代数式表示![]() 为:
为:![]() =;
=;
(2)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润为60万元?
【答案】(1)6-x;(2)公司每年国内销售量为2千件,国外的销售量为4千件或国内销售量为6千件,国外的销售量为0件时,可使公司每年的总利润为60万元.
【解析】
(1)由于该公司的年产量为6000件,每年可在国内、国外市场上全部售完,可得国内销售量+国外销售量=6千件,即x+t=6,变形即为t=6-x;
(2)根据平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系y2=![]() 及t=6-x即可求出y2与x的函数关系:当0≤x≤3时,y2=5x+80;当3<x≤6时,y2=100;根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分二种情况讨论:①
及t=6-x即可求出y2与x的函数关系:当0≤x≤3时,y2=5x+80;当3<x≤6时,y2=100;根据总利润=国内销售的利润+国外销售的利润,结合函数解析式,分二种情况讨论:①![]() ;②
;②![]() 即可.
即可.
(1)由题意,得x+t=6,
∴t=6-x;
(2)设国内平均每件产品的利润为y1,则有y1=![]()
设平均每件产品的利润为y2则有y2=![]() 且t=6-x,
且t=6-x,
∴y2=![]() ,
,
分两种情况:
①当0≤x≤3时,(15x+90)x+(5x+80)(6-x)=600;
解得,![]() ,
,![]() (舍去)
(舍去)
∴t=6-x=4,
所以,公司每年国内销售量为2千件,国外的销售量为4千件时,可使公司每年的总利润为60万元.
②当3<x≤6时,(-5x+130)x+100(6-x)=600
解得,![]() ,
,![]() (舍去)
(舍去)
∴t=6-x=0,
所以,公司每年国内销售量为6千件,国外的销售量为0件时,可使公司每年的总利润为60万元.


科目:初中数学 来源: 题型:
【题目】甲、乙两个学校乐团,决定向某服装厂购买同样的演出服。下面是服装厂给出的演出服装的价格表:经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,按每人一套的标准两个乐团共需花费5600元。请回答以下问题:
购买服装的套数 | 1~39套(含39套) | 40~79套(含79套) | 80套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少人?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友,这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖。请写出所有的抽调方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
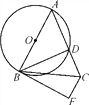
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中休息了-段时间后,仍按原速行驶他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示,
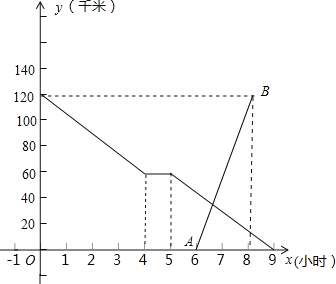
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/小时;
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇,则他出发的时间x应在什么范围?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.
求证:(1)△ABC≌△DEF;
(2)如果∠ACB=25°,求∠AGF的度数?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com