
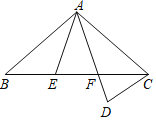
【题目】如图,![]() ,
,![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 于点
于点![]() ,
,![]() 为
为![]() 中点,
中点,![]() 于
于![]() ,
,![]() .下列说法正确的是( )
.下列说法正确的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .
.

A.①③④B.②③C.①②③D.①②③④
【答案】C
【解析】
根据平行线的性质以及角平分线的定义即可得到![]() 从而根据三角形的内角和定理得到
从而根据三角形的内角和定理得到![]() ,即可判断①正确性;根据等角的余角相等可知
,即可判断①正确性;根据等角的余角相等可知![]() ,再由角平分线的定义与等量代换可知
,再由角平分线的定义与等量代换可知![]() ,即可判断②正确性;通过面积的计算方法,由等底等高的三角形面积相等,即可判断③正确性;通过角度的和差计算先求出
,即可判断②正确性;通过面积的计算方法,由等底等高的三角形面积相等,即可判断③正确性;通过角度的和差计算先求出![]() 的度数,再求出
的度数,再求出![]() ,再由三角形内角和定理及补角关系即可判断④是否正确.
,再由三角形内角和定理及补角关系即可判断④是否正确.
①中,∵AB∥CD,
∴![]() ,
,
∵∠BAC与∠DCA的平分线相交于点G,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴AG⊥CG,
则①正确;
②中,由①得AG⊥CG,
∵![]() ,
,![]() ,
,
∴根据等角的余角相等得![]() ,
,
∵AG平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
则②正确;
③中,根据三角形的面积公式,∵![]() 为
为![]() 中点,∴AF=CF,∵
中点,∴AF=CF,∵![]() 与
与![]() 等底等高,∴
等底等高,∴![]() ,则③正确;
,则③正确;
④中,根据题意,得:在四边形GECH中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵CG平分∠ECH,
∴![]() ,
,
根据直角三角形的两个锐角互余,得![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,则④错误.
,则④错误.
故正确的有①②③,
故选:C.


科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为_____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6000件,若在国内市场销售,平均每件产品的利润与国内销售量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) |
|
|
若在国外销售,平均每件产品的利润与国外的销售数量![]() 的关系如下表:
的关系如下表:
销售量 |
|
|
单件利润(元) | 100 |
|
(1)用![]() 的代数式表示
的代数式表示![]() 为:
为:![]() =;
=;
(2)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润为60万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E、 F为AB上的一点,CF⊥AD于H,下列判断正确的有( )

A.AD是△ABE的角平分线B.BE是△ABD边AD上的中线
C.AH为△ABC的角平分线D.CH为△ACD边AD上的高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,分别交l1、l2于A. B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A. B重合,设∠DAB=∠α.

(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚做游戏一个不透明的布袋里装有4个大小、质地均相同的乒乓球,球上分别标有数字1,2,3,4,随机从布袋中摸出一个乒乓球,记下数字后放回布袋里,再随机从布袋中摸出一个乒乓球,若这两个乒乓球上的数字之和能被4整除则小明赢;若两个乒乓球上的数字之和能被5整除则小刚赢;这个一个对游戏双方公平的游戏吗?请列表格或画树状图说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com