
【题目】已知直线l1∥l2,分别交l1、l2于A. B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A. B重合,设∠DAB=∠α.

(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明。
【答案】(1)见解析;(2)∠α+∠APC+∠PCB=180°,理由见解析;
【解析】
(1)先根据平行线的性质得出∠α=∠PBC.再由∠APC是△PBC的一个外角得出∠APC=∠PBC+∠PCB,通过等量代换即可得出结论;
(2)由l1∥l2可知∠α=∠PBC,再根据三角形内角和定理得出∠PBC+∠PCB+∠APC=180°,利用等量代换即可得出结论.
(1)证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠APC是△PBC的一个外角,
∴∠APC=∠PBC+∠PCB,
∴∠APC=∠α+∠PCB.
(2)三个角的关系为:∠α+∠APC+∠PCB=180°.
证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠PBC+∠PCB+∠APC=180°,
∴∠α+∠PCB+∠APC=180°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)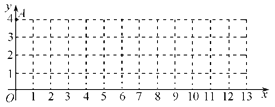
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+(____)2=﹣
x+(____)2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 与坐标原点重合,其边长为2,点
与坐标原点重合,其边长为2,点![]() ,点
,点![]() 分别在
分别在![]() 轴,
轴, ![]() 轴的正半轴上.函数
轴的正半轴上.函数![]() 的图像与
的图像与![]() 交于点
交于点![]() ,函数
,函数![]() 为常数,
为常数, ![]() )的图像经过点
)的图像经过点![]() ,与
,与![]() 交于点
交于点![]() ,与函数
,与函数![]() 的图像在第三象服内交于点
的图像在第三象服内交于点![]() ,连接
,连接![]() .
.
(1)求函数![]() 的表达式,并直接写出
的表达式,并直接写出![]() 两点的坐标;
两点的坐标;
(2)求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究活动一:
如图1,正方形ABCD和正方形QMNP,∠M=∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E,线段ME与线段MF的数量关系是 .(不必证明,直接给出结论即可)
探究活动二:
如图2,将上题中的“正方形”改为“矩形”,且AB=mBC,其他条件不变(矩形ABCD和矩形QMNP,∠M=∠B,M是矩形ABCD的对称中心,MN交AB于F,QM交AD于E),探究并证明线段ME与线段MF的数量关系;
探究活动三:
根据前面的探索和图3,平行四边形ABCD和平行四边形QMNP中,若AB=mBC,∠M=∠B,M是平行四边形ABCD的对称中心,MN交AB于F,QM交AD于E,请探究并证明线段ME与线段MF的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ΔABC和ΔDCE均是等边三角形,点B,C,E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论: ①AE=BD;②AG =BF;③FG∥BE;④CF=CG.其中正确的结论为____________.
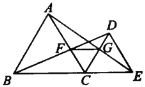
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com