
【题目】探究活动一:
如图1,正方形ABCD和正方形QMNP,∠M=∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E,线段ME与线段MF的数量关系是 .(不必证明,直接给出结论即可)
探究活动二:
如图2,将上题中的“正方形”改为“矩形”,且AB=mBC,其他条件不变(矩形ABCD和矩形QMNP,∠M=∠B,M是矩形ABCD的对称中心,MN交AB于F,QM交AD于E),探究并证明线段ME与线段MF的数量关系;
探究活动三:
根据前面的探索和图3,平行四边形ABCD和平行四边形QMNP中,若AB=mBC,∠M=∠B,M是平行四边形ABCD的对称中心,MN交AB于F,QM交AD于E,请探究并证明线段ME与线段MF的数量关系.

【答案】(1)ME=MF.(2) ME=mMF.理由见解析;(3)ME=mMF.理由见解析.
【解析】
(1)过点M作MH⊥AB于H,MG⊥AD于G,连接AM,首先证明M是正方形ABCD对角线的交点,然后证明△MHF≌△MGE,利用全等三角形的性质得到ME=MF;
(2)过点M作ME⊥AB于E,MG⊥AD于G,利用矩形ABCD性质和已知条件证明∠HMF=∠GME,∠MGE=∠MHF,得出△MGE∽△MHF,然后利用相似三角形的性质即可求解;
(3)平行四边形ABCD和平行四边形QMNP中,∠M=∠B,AB=mBC,由于M是平行四边形ABCD的对称中心,MN交AB于F,AD交QM于E,则ME=mMF.证明方法和(1)(2)类似.
(1)ME=MF.
理由:如图1,过点M作MH⊥AB于H,MG⊥AD于G,连接AM,[来源:学*科*网Z*X*X*K]
则∠MHF=∠MGE=90°,
∵M是正方形ABCD的对称中心,
∴AM平分∠BAD,
∴MH=MG,
在正方形ABCD中,∠DAB=90°,而∠MHA=∠MGA=90°,
∴∠EMF=∠HMG=90°,
∴∠FMH=∠EMG,
在△MHF和△MGE中,
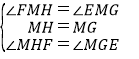
∴△MHF≌△MGE(ASA),
∴MF=ME,
故答案为:MF=ME;
(2)ME=mMF.
理由:如图2,过点M作MG⊥AB于G,MH⊥AD于H,
则∠MHE=∠MGF=90°,
在矩形ABCD中,∠A=90°,
∴在四边形GMHA中,∠GMH=90°,
又∵∠EMF=90°,
∴∠HME=∠GMF,
又∵∠MGF=∠MHE=90°,
∴△MGF∽△MHE,
∴![]() ,
,
又∵M是矩形ABCD的对称中心,
∴MG=![]() BC,MH=
BC,MH=![]() AB,
AB,
∵AB=mBC,
∴![]() =m,
=m,
∴ME=mMF;
(3)ME=mMF.
理由:如图3,过点M作MG⊥AB于G,MH⊥AD于H,
则∠MHE=∠MGF=90°,
在平行四边形ABCD中,∠A+∠B=180°,而∠EMF=∠B,
∴∠A+∠EMF=180°,
又∵在四边形AGMH中,∠A+∠HMG=180°,
∴∠EMF=∠GMF,
又∵∠MGF=∠MHE=90°,
∴△MGF∽△MHE,
∴![]() ,
,
又∵M是矩形ABCD的对称中心,
∴MG=![]() BC,MH=
BC,MH=![]() AB,
AB,
∵AB=mBC,
∴![]() ,
,
∴ME=mMF.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
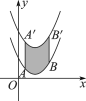
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,分别交l1、l2于A. B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A. B重合,设∠DAB=∠α.

(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
王同学 | 60 | 75 | 100 | 90 | 75 |
李同学 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
王同学 | 80 | 75 | 75 | _____ |
李同学 |
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚做游戏一个不透明的布袋里装有4个大小、质地均相同的乒乓球,球上分别标有数字1,2,3,4,随机从布袋中摸出一个乒乓球,记下数字后放回布袋里,再随机从布袋中摸出一个乒乓球,若这两个乒乓球上的数字之和能被4整除则小明赢;若两个乒乓球上的数字之和能被5整除则小刚赢;这个一个对游戏双方公平的游戏吗?请列表格或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
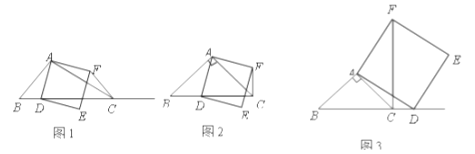
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com