
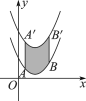
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
【答案】y=![]() (x-2)2+4
(x-2)2+4
【解析】
先根据二次函数图象上点的坐标特征求出A、B两点的坐标,再过A作AC∥x轴,交B′B的延长线于点C,则C(4,1![]() ),AC=4-1=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
),AC=4-1=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
∵函数y=![]() (x-2)2+1的图象过点A(1,m),B(4,n),
(x-2)2+1的图象过点A(1,m),B(4,n),
∴m=![]() (1-2)2+1=1
(1-2)2+1=1![]() ,n=
,n=![]() (4-2)2+1=3,
(4-2)2+1=3,
∴A(1,1![]() ),B(4,3),
),B(4,3),
过A作AC∥x轴,交B′B的延长线于点C,则C(4,1![]() ),
),
∴AC=4-1=3,
∵曲线段AB扫过的面积为9(图中的阴影部分),
∴ACAA′=3AA′=9,
∴AA′=3,
即将函数y=![]() (x-2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
(x-2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y=![]() (x-2)2+4.
(x-2)2+4.
故答案是:y=![]() (x-2)2+4.
(x-2)2+4.


科目:初中数学 来源: 题型:
【题目】有一块面积为100cm2的正方形纸片.
(1)该正方形纸片的边长为 cm(直接写出结果);
(2)小丽想沿着该纸片边的方向裁剪出一块面积为90cm2的长方形纸片,使它的长宽之比为4:3.小丽能用这块纸片裁剪出符合要求的纸片吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)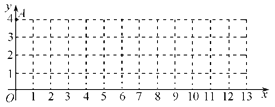
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形.

(1)若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个的等式,这个等式可以为 ;
(2)请利用(1)中的等式解答下列问题:
①若三个实数a,b,c满足a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=32,x2+4y2+9z2=45,求2xy﹣3xz﹣6yz的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
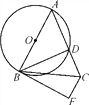
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
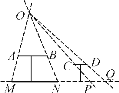
【题目】如图,AB是公园的一圆桌的主视图,MN表示该桌面在路灯下的影子,CD则表示一个圆形的凳子.
(1)请在图中标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径与桌面距地面的距离为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+(____)2=﹣
x+(____)2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究活动一:
如图1,正方形ABCD和正方形QMNP,∠M=∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E,线段ME与线段MF的数量关系是 .(不必证明,直接给出结论即可)
探究活动二:
如图2,将上题中的“正方形”改为“矩形”,且AB=mBC,其他条件不变(矩形ABCD和矩形QMNP,∠M=∠B,M是矩形ABCD的对称中心,MN交AB于F,QM交AD于E),探究并证明线段ME与线段MF的数量关系;
探究活动三:
根据前面的探索和图3,平行四边形ABCD和平行四边形QMNP中,若AB=mBC,∠M=∠B,M是平行四边形ABCD的对称中心,MN交AB于F,QM交AD于E,请探究并证明线段ME与线段MF的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com