
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+(____)2=﹣
x+(____)2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
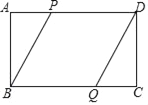
【题目】如图,矩形ABCD中,点P是线段AD上任意一点,点Q为BC上一点,且AP=CQ.
(1)求证:BP=DQ;
(2)若AB=4,且当PD=5时四边形PBQD为菱形.求AD为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
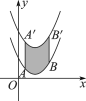
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
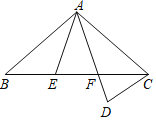
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,分别交l1、l2于A. B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A. B重合,设∠DAB=∠α.

(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
王同学 | 60 | 75 | 100 | 90 | 75 |
李同学 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
王同学 | 80 | 75 | 75 | _____ |
李同学 |
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com