
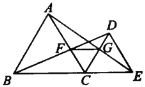
【题目】如图,已知ΔABC和ΔDCE均是等边三角形,点B,C,E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论: ①AE=BD;②AG =BF;③FG∥BE;④CF=CG.其中正确的结论为____________.
【答案】①②③④
【解析】
首先由SAS判定△BCD≌△ACE,即可证得①正确;又由全等三角形的对应角相等,得到∠CBD=∠CAE,根据ASA,证得△BCF≌△ACG,即可得到②正确,同理证得CF=CG,则④正确,可得∠FCE=60°,可得△CFG是等边三角形,则可得∠CFG=∠FCB,则FG∥BE,可得③正确.
解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
∴△BCD≌△ACE(SAS),
∴AE=BD,(①正确)
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,AC=BC,
∴△BCF≌△ACG(ASA),
∴AG=BF,(②正确)
∴CF=CG(④正确),且∠ACD=60°
∴△CFG是等边三角形,
∴∠CFG=∠FCB=60°,
∴FG∥BE,(③正确)
正确的有①②③④.


科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,分别交l1、l2于A. B两点,点C在直线l2上且在点B的右侧,点D在直线l1上且在点A左侧,点P是直线l3上的动点,且不与A. B重合,设∠DAB=∠α.

(1)如图1,当点P在线段AB上时,求证:∠APC=∠α+∠PCB;
(2)如图2,当点P在线段BA的延长线上时,请写出∠α、∠APC、∠PCB三个角之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
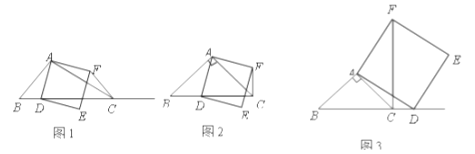
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
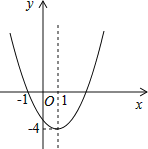
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com