
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
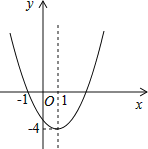
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
【答案】D
【解析】
试题分析:根据对称轴及抛物线与x轴交点情况,结合二次函数的性质,即可对所得结论进行判断.
解:A、观察图象,可知抛物线的对称轴为直线x=1,则图象关于直线x=1对称,正确,故本选项不符合题意;
B、观察图象,可知抛物线的顶点坐标为(1,﹣4),又抛物线开口向上,所以函数y=ax2+bx+c(a≠0)的最小值是﹣4,正确,故本选项不符合题意;
C、由图象可知抛物线与x轴的一个交点为(﹣1,0),而对称轴为直线x=1,所以抛物线与x轴的另外一个交点为(3,0),则﹣1和3是方程ax2+bx+c=0(a≠0)的两个根,正确,故本选项不符合题意;
D、由抛物线的对称轴为x=1,所以当x<1时,y随x的增大而减小,错误,故本选项符合题意.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 与坐标原点重合,其边长为2,点
与坐标原点重合,其边长为2,点![]() ,点
,点![]() 分别在
分别在![]() 轴,
轴, ![]() 轴的正半轴上.函数
轴的正半轴上.函数![]() 的图像与
的图像与![]() 交于点
交于点![]() ,函数
,函数![]() 为常数,
为常数, ![]() )的图像经过点
)的图像经过点![]() ,与
,与![]() 交于点
交于点![]() ,与函数
,与函数![]() 的图像在第三象服内交于点
的图像在第三象服内交于点![]() ,连接
,连接![]() .
.
(1)求函数![]() 的表达式,并直接写出
的表达式,并直接写出![]() 两点的坐标;
两点的坐标;
(2)求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面的证明过程补充完整.
已知:如图,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 延长线上,
延长线上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
求证:![]() .
.

证明:在![]() 中,
中,
![]() ( ).
( ).
又![]() (已知),
(已知),
![]()
![]() .
.
![]() 是
是![]() 的角平分线,
的角平分线,
![]() ( ).
( ).
![]() (等量代换).
(等量代换).
![]() .
.
![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ΔABC和ΔDCE均是等边三角形,点B,C,E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论: ①AE=BD;②AG =BF;③FG∥BE;④CF=CG.其中正确的结论为____________.
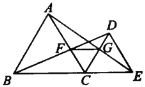
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠CB.∠A-∠B=∠C
C.∠A=∠B=2∠CD.∠A:∠B:∠C=1:2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
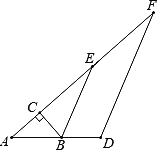
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划一个月安装新式儿童小机器人玩具480台.由于熟练工不够,工厂决定招聘一些新工人,新工人经过培训后上岗.调研部门发现:1名熟练工和2名新工人每天可安装16台小机器人玩具;3名熟练工和4名新工人每天可安装40台小机器人玩具.
(1)每名熟练工和新工人每天分别可以安装多少台小机器人玩具?
(2)如果工厂招聘![]() 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一个月的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一个月的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com