
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=﹣x2+2x+3.(2)图象见解析;(3)点N的坐标为(1,0)或(﹣7,0).
【解析】
(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求得b,c的值即可;
(2)依据抛物线解析式为y=-x2+2x+3,列表,描点,连线即可;
(3)先利用配方法求得点D的坐标,当∠DNA=90°时,DN⊥OA,可得到点N的坐标,从而得到AN=2,然后再求得AD的长;当∠N′DA=90°时,依据sin∠DN′A=sin∠ADN可求得AN′的长,从而可得到N′的坐标.
解:(1)将x=0代入AB的解析式y=﹣x+3得:y=3,
∴B(0,3).
将y=0代入AB的解析式y=﹣x+3得:﹣x+3=0,
解得x=3,
即A(3,0).
将点A和点B的坐标代入y=﹣x2+bx+c,得:
![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)列表:
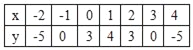
抛物线的图象如下:
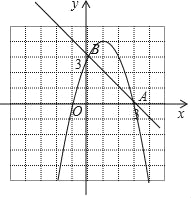
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
①当∠DNA=90°时,如图所示:

∵∠DNA=90°时,
∴DN⊥OA.
又∵D(1,4)
∴N(1,0).
∴AN=2.
∵DN=4,AN=2,
∴AD=2![]() .
.
②当∠N′DA=90°时,则∠DN′A=∠NDA.
∴![]() ,
,
即![]() ,
,
解得:AN′=10.
∵A(3,0),
∴N′(﹣7,0).
综上所述,点N的坐标为(1,0)或(﹣7,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
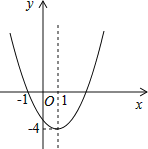
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
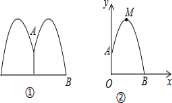
【题目】如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如下图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),则该抛物的解析式为__________________________。如果不考虑其他因素,那么水池的半径至少要______m,才能使喷出的水流不至落到池外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资W(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )

A. 8.4小时 B. 8.6小时 C. 8.8小时 D. 10小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com