
【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

【答案】(1)OF⊥OD,证明详见解析;(2)∠EOF=60°.
【解析】
(1)由OD平分∠BOE、OF平分∠AOE,可得出∠FOE=![]() ∠AOE、∠EOD=
∠AOE、∠EOD=![]() ∠EOB,根据邻补角互补可得出∠AOE+∠EOB=180°,进而可得出∠FOD=∠FOE+∠EOD=90°,由此即可证出OF⊥OD;
∠EOB,根据邻补角互补可得出∠AOE+∠EOB=180°,进而可得出∠FOD=∠FOE+∠EOD=90°,由此即可证出OF⊥OD;
(2)由∠AOC:∠AOD=1:5结合邻补角互补、对顶角相等,可求出∠BOD的度数,根据OD平分∠BOE、OF平分∠AOE,可得出∠BOE的度数以及∠EOF=![]() ∠AOE,再根据邻补角互补结合∠EOF=
∠AOE,再根据邻补角互补结合∠EOF=![]() ∠AOE,可求出∠EOF的度数.
∠AOE,可求出∠EOF的度数.
(1)OF⊥OD.
证明:∵OD平分∠BOE,OF平分∠AOE,
∴∠FOE=![]() ∠AOE,∠EOD=
∠AOE,∠EOD=![]() ∠EOB.
∠EOB.
∵∠AOE+∠EOB=180°,
∴∠FOD=∠FOE+∠EOD=![]() (∠AOE+∠EOB)=90°.
(∠AOE+∠EOB)=90°.
∴OF⊥OD.
(2)∵∠AOC:∠AOD=1:5,∠AOC=∠BOD,
∴∠BOD:∠AOD=1:5.
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°.
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF=![]() ∠AOE.
∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,
∴∠EOF=60°.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度数;
(2)∠FEG的度数;
(3)∠1和∠2的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. 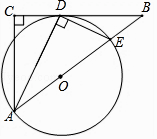
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
① ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
…
(1)请按以上规律写出第⑤个等式:;
(2)猜想并写出第n个等式:;
(3)请证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com